Over the past three chapters, we discussed some key statistical tools that help in analyzing individual risks of a security as well as in understanding the relationship between two securities. In this chapter, we will talk about another important statistical metric, Beta.
Beta
When it comes to financial markets, beta is an extremely popular and important statistical metric of measuring risk. What exactly does beta measure? Well, beta measures the sensitivity of the returns of a security (the dependent variable) to the returns of the market (the independent variable). Beta provides information not only about the direction but also about the magnitude. Speaking of direction, beta tells us whether the returns of the security move in the direction or against the direction of the market returns. That is, when market returns are positive, are the stock returns positive or negative, and vice versa. Speaking of magnitude, beta tells us the potential theoretical change in the returns of a security for a given change in the market returns. That is, if the market rises by, say, 1%, by what percent will the stock rise or fall? So essentially, by capturing the sensitivity of security returns to market returns, beta helps in measuring the systematic risk. Mathematically, Beta is calculated as:
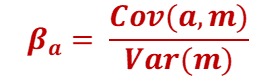
where,
- βa = = Beta of security A
- Cov(a,m) = Covariance between the returns of security A and that of market M
- Var(m) = Variance of market returns
As both covariance and variance are expressed in squared units, the beta is a standardized measure. As a result, one can compare the value of beta across securities.
Keep in mind that the beta of the market is equal to 1. Why so? Well, to understand that, let us do a few calculations using the above formula
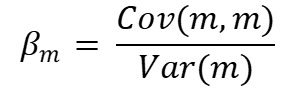
Let us now individually solve the numerator and denominator of the above equation (it is assumed that you have read the prior three chapters and know how covariance and variance are calculated):

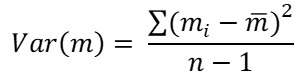
See that the above two equations are the same. Here is an important property worth remembering: covariance of a security with itself is equal to the variance of that security. So, the covariance of the market with itself is equal to the variance of the market. Substituting the values of the above two equations into the formula of market beta would fetch a result of 1. It is worth keeping this in memory.
A question that you might ask is, when we say market, what market are we referring to? Well, if the underlying security whose beta you are interested in calculating is a stock, the market usually refers to the benchmark stock market index of a country. In the case of India, this is either the Nifty or the Sensex. So, if you are interested in calculating the beta of, say, Tata Steel based on the historical price data of the last one month, you would do so against Nifty or Sensex. Beta of a stock can also be computed against the sectoral index of which it is a part of. For instance, you can calculate the beta of ICICI bank against Bank Nifty as well, because ICICI bank is a component of the Bank Nifty index. The difference between calculating beta of ICICI bank against Bank Nifty as against Nifty is that the former will tell us how sensitive ICICI bank is relative to the banking index, while the latter will tell how sensitive ICICI bank is to the market as a whole. Goes without saying, if you measure beta of a stock relative to a sectoral index, ensure that you do so against a relevant index. For instance, it makes sense to calculate beta of ICICI bank against Bank Nifty but not against, say, Pharma index.
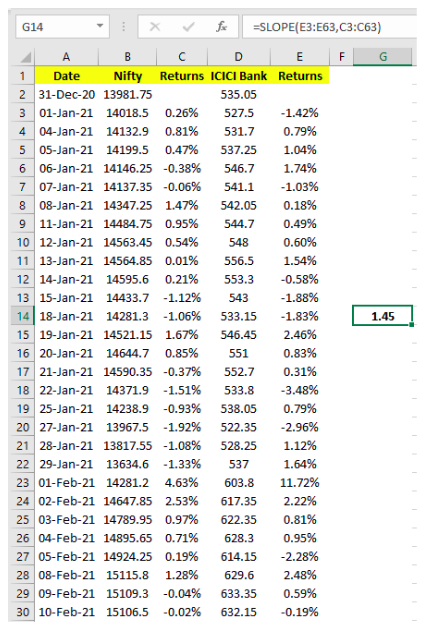
As beta of the market is 1, this value becomes a reference when looking at the beta of a security. The beta of a security could be either above 1 or below 1. It could also be zero or negative. While beta can be manually calculated, doing so is very time consuming. Hence, the best way to solve for beta is through Microsoft Excel. Let us illustrate this using a real world example. Let us calculate the beta of ICICI Bank based on the returns of the daily closing price for the period 1-Jan to 31-Mar 2021.
In the above example, look at the formula bar to see how beta has been calculated in cell G14, based on the returns of ICICI bank and the returns of the market. The Excel function to calculate beta is =SLOPE(). Inside the parenthesis, you would include all the returns of the security (the dependent variable, ICICI bank in our case) for the period under consideration as well as all the returns of the market (the independent variable, Nifty in our case). The two must be separated by a comma. It is especially important to keep in mind that the order in which the returns are inputted matters. Above, because we are calculating the beta of ICICI bank (the dependent variable) relative to Nifty (the independent variable), the returns of ICICI bank must be inputted first followed by that of Nifty. In our case, see that beta turned out to be 1.45. What does this suggest? Well, before talk about this, let us put down a few guidelines relating to beta of a stock:
Let us first understand the directional implication of the beta of a stock:
Let us now understand the magnitude implication of the beta of a stock:
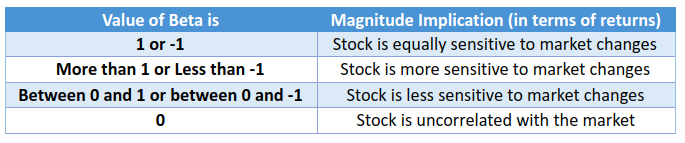
Let us now combine the above two tables to understand how to interpret the value of a beta. Let us do this using a few hypothetical values for beta:
Notice in the above table how the beta captures both the direction and the magnitude impact of a change in market return on the stock return. In short:
- If the absolute value of beta is 1, it means the stock is as volatile as the market
- If the absolute value of beta is more than 1, it means the stock is more volatile than the market
- If the absolute value of beta is less than 1, it means the stock is less volatile than the market
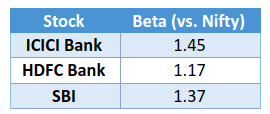
Coming back to our earlier example of ICICI bank, we saw that the beta turned out to be 1.45. This means, based on the historical daily returns of the first three months of 2021, it can be inferred that ICICI bank has been 45% more volatile than Nifty. Furthermore, as the beta is positive, ICICI bank has moved in the same direction as the Nifty. Similarly, for the same period, let us calculate the beta of two more banks, say HDFC bank and SBI. The results are displayed in the table below:
As can be seen, all the three banks have been more volatile than Nifty and have moved in the same direction as the Nifty. Among the three, ICICI has been the most volatile while HDFC bank has been the least volatile. See that beta can be compared across securities because it is a standardized measure. Now that we understand beta and how to interpret it, let us move ahead and talk about the importance of beta.
Before proceeding though, keep in mind that beta is applicable not only to stocks. Instead, it can be applied to other asset classes as well. For example, you could measure the beta of gold versus a commodity index, such as the S&P GSCI or the CRB index.
Importance of Beta
As beta measures the direction and volatility of a stock vis-à-vis the market, it is an important statistical metric to gauge systematic risk of a security. Because the risk appetite and tolerance level vary from one trader or investor to another, it is important to be aware of a stock’s volatility relative to the market as a whole. If a trader or an investor has a greater tolerance for risk and prefers high returns over stability, a higher proportion of equity capital could be deployed into high beta stocks (beta >1) with the objective of maximizing portfolio returns. On the other hand, if a trader or investor is risk averse and prefers stable returns, a greater proportion of equity capital could be deployed into low beta stocks (beta <1) with the objective of reducing exposure to market risk. Meanwhile, a balanced trader or investor could prefer putting half of equity capital into high beta stocks and the rest into low beta stocks to balance out the portfolio beta.
Additionally, depending on market outlook, a trader or investor could decide to alter the proportion of stocks with high and low betas. As an example, if a trader or investor has a bullish outlook on the market, a greater proportion of equity capital could be deployed into stocks with high beta, with the objective of maximizing returns. On the other hand, if a trader or investor is not bullish on the market and believes that volatility could increase going forward, the proportion of stocks with high betas could be reduced from the portfolio in favour of stocks that have low beta, to limit drawdowns.
As you can sense by now, beta forms an important part of portfolio management and is a widely used metric to measure portfolio risks. Beta also forms a key component of the Capital Asset Pricing Model (CAPM), a model that is widely used in finance to determine the theoretical required rate of return for a particular security. We will talk about CAPM later in this module.
Recapping and the way ahead
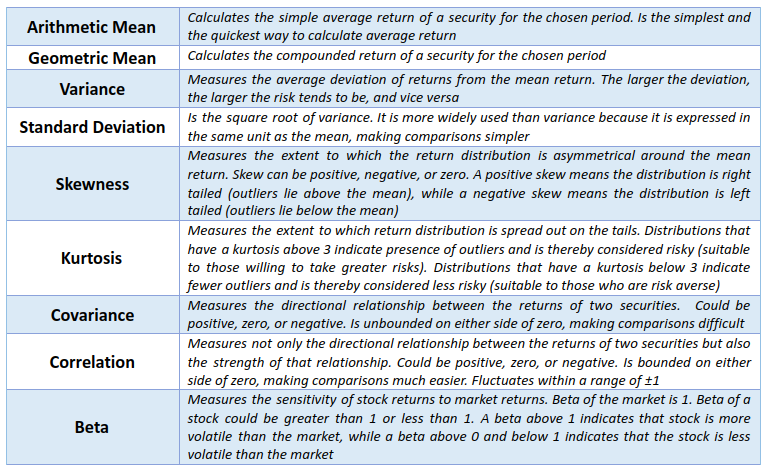
Over the past four chapters, we have explained several important statistical tools to gauge risk (and return). We have covered the mean, variance & standard deviation, skewness & kurtosis, covariance & correlation, and beta. That covers the key statistical metrics of measuring individual security risks that we wanted to talk about in this module. Let us quickly recap these tools before proceeding to the next chapter:
In the coming chapters, we will focus on portfolio risks (and returns). After that, we will turn our attention towards trading risks and how to manage them.
Next Chapter
Comments & Discussions in
FYERS Community