In the previous chapter, we introduced the concept of Volatility. We saw things such as what volatility is, the most widely used measure of volatility, how to calculate and interpret standard deviation, how to annualize standard deviation, how to convert annualized standard deviation into the time period that you desire, how to calculate standard deviation in Microsoft Excel, what historical volatility is, and what implied volatility is. Given that we now understand the basics of volatility, it is time to refocus on Options Greeks and talk about our next Greek: Vega.
Introducing Vega
So far, we have seen two of the five Option Greeks: Delta and Gamma. We saw that Delta measures the rate of change in option price for every 1 point change in the value of the underlying asset, while Gamma measures the rate of change in Delta for every 1 point change in the value of the underlying asset. By now, we realize that volatility is a major component impacting the pricing of an option. Using Vega, we can quantify the extent to which volatility impacts option price. Vega can be defined as the change in option price for every 1 percentchange in Implied Volatility (IV). We use percentage here becauseImplied Volatility is expressed as a percentage. So, if Implied Volatility (IV) changes by 1%, option price will change by the value of the Vega. Similarly, if Implied Volatility (IV) changes by 2%, option price will change by the value of 2 times the Vega, and so forth. As an example, if the Vega of an option is 0.10 and if the Implied Volatility of a stock has changed from, say, 15% to 16%, the option price would change by the value of one Vega, i.e. 0.10.
Rising Implied Volatility leads to an increase in the price of an option, and vice versa. Think about this for a moment. We defined Vega as a tool which measures the rate of change in option price for a 1% change in Implied Volatility. From this, we can see that the higher the implied volatility, the higher would be the rate of change in option price, and vice versa. For instance, in the example above, we saw that a 1% increase in IV led to the option price increasing by the value of 1 Vega i.e. 0.10. However, if the IV were to increase by, say,5%, then the option price would have increased by the value of five times the Vega i.e. 0.50. Another way to think about why higher volatility leads to an increase in the price of an option would be to think from an option seller’s perspective. In the earlier chapters, we saw that the seller has an obligation instead of a right to fulfil the option contract. Because of this feature which exposes a seller to potentially unlimited losses, the seller would command a higher option price during times when volatility is increasing, to compensate for the higher risk that he is taking.
As was stated above, rising Implied Volatility leads to an increase in the price of an option, and vice versa. This applies to both call options and put options. So, a buyer of an option, be it a call or a put, will benefit when IVs go up and stand to lose when IVs go down. On the other hand, the seller of an option will benefit when IVs go down and suffer when IVs go up. From this, it can be said that the buyer of an option must have a bullish view on volatility, while the seller of an option must have a bearish (or a neutral) view on volatility.Because the buyer benefits when the price of an option goes up and because IV is positively correlated to option price, Vega is positive for long options. On the other hand, because the seller benefits when the price of an option goes down and because IV is positively correlated to option price, Vega is negative for short options.In other words, when you are long options, you tend to havea long Vega exposure. And when you are short options, you tend to havea short Vega exposure.
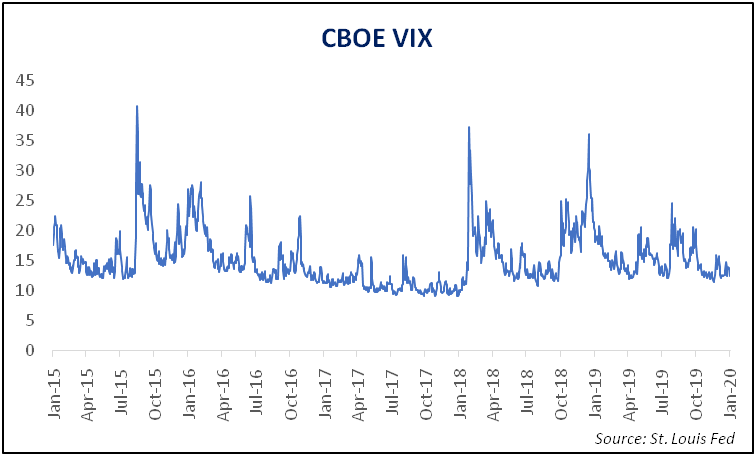
Having a long or short exposure on Vega has implications. This is especially true in case of having a short Vega exposure, given that it opens the probability of being exposed to unlimited risk (remember, the risk to an option seller is potentially unlimited). Keep in mind that IVs usually tend to rise sharply and swiftly than they fall. The chart below shows this:
The above chart is the chart of CBOE VIX. Here, CBOE stands for Chicago Board Options Exchange, while VIX stands for Volatility index. We will talk more about CBOE VIX in a later chapter. For now, just remember that CBOE VIX is derived from the S&P 500 index options and measures the 30-day implied volatility of the US stock market. It is one of the most widely tracked measure of volatility and tells us about the mood and sentiment of market participants. A rising VIX usually coincides with a fall in the stock market and hence is a sign of increasing fear and pessimism.It indicates that market participants expect volatility to pick up in the coming days. On the other hand, a falling VIX usually coincides with a rising market and hence is a sign of calm and optimism. It indicates that market participants expect volatility to contract in the days ahead.Coming back to our discussion, notice in the above chart that there is a tendency for VIX to spike sharply in a brief span of time. On the other hand, observe that the declines in VIX are usually gradual. Because rising volatility works against an option seller and given how sharply it can rise in a quick span of time, short Vega positions need to be carefully monitored to ensure that their exposure are within tolerable levels.
Lastly, keep in mind that Vega is identical for call and put options that have the same underlying, same expiration, and same strike price. What differs however, is the implied volatility. Also, remember that Vega impacts only the time value component of the option price, and not the intrinsic value.
Impact of Time to Expiration on Vega
The higher the time to expiration of an option contract, the higher would be the Vega of the option, all else equal. This is because the higher the time to expiration, the greater would be the uncertainty in terms of whether the option would expire ITM. And the greater the uncertainty, the greater is the room for IVs to have an impact on the price of an option. However, as we move closer to expiration, the uncertainty about whether the option would expire ITM starts to reduce. This in turn causes the Vega to reduce as well. The chart below shows the impact of time left to expiration on Vega. Here, we have assumed a few things as follows:
- Strike price = ₹100
- Underlying price = ₹100
- Implied Volatility = 20%
- Dividend = 0
- Risk-free rate = 5%
Each of these variables has remained constant throughout. The only changing variable is the time left to expiration. Observe in the chart that Vega was 0.37 when there was 1 year left to expiration. However, observe that as the time left to expiration reduced, so did the Vega. With just 1 day left to expiration, Vega is just 0.02. As said, the reason why this happens is because the greater the time there is to expiration, the greater is the room for IVs to have an impact on the option price.
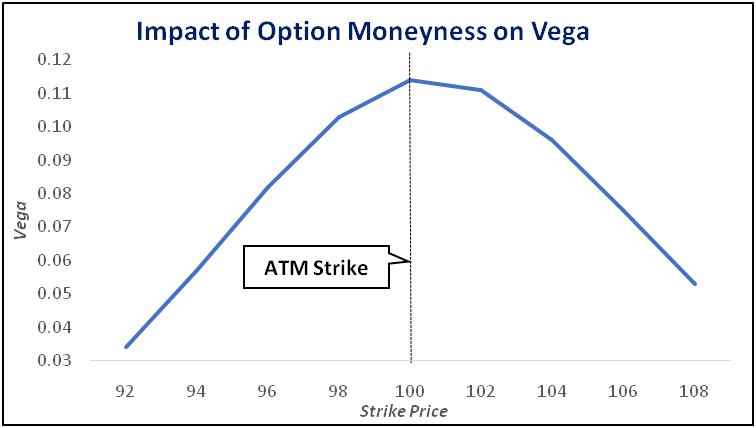
Impact of Option Moneynesson Vega
Vega tends to be highest for options that are ATM. As the option start moving either ITM or OTM, Vega starts declining. Vega tends to be very low in case of options that are deep ITM or deep OTM. Why does this happen? One of the major reasons why this happens is becauseof the time value component of an option price. As we shall see in the next chapter, ATM options tend to have the highest time value (in absolute terms). As the options start moving away from being ATM, their time value starts reducing (meaning the time value in absolute terms starts moving towards zero). And as the time value reduces, so does the Vega. Keep in mind that options that are deep ITM or deep OTM are not much impacted by change in IVs because their Vega tends to be lower. The maximum impact of change in IVs tends to occur for options that are ATM or close to being ATM because they tend to have the highest Vega. The chart below shows this.
In the above chart, we have assumed the following:
- Underlying price = ₹100
- Time to Expiration = 30 days
- Implied Volatility = 20%
- Dividend = 0
- Risk-free rate = 5%
Notice in the chart how the Vega moves around the ATM options - being the highest when the option is ATM and startingto reduce as the option moves away from being ATM. Logically speaking, remember that everything boils down to whether the option will expire ITM on the expiration date. When the option is ATM, the uncertainty as to where it will expire - ITM or OTM - is the highest and hence, the Vega is also at its highest. However, as the option starts moving away from being ATM, the uncertainty as to where it will expire starts reducing, causing the Vega to reduce as well. For instance, if an option moves ITM, the odds of it expiring ITM start moving above 50% and towards 100%. Conversely, if an option moves OTM, the odds of it expiring ITM start moving below 50% and towards 0%. The closer the probability of an option expiring ITM moves toward the extremes (i.e. 0% or 100%), the lower will the Vega be.
Impact of changes in Volatility on Option Price
By now, we clearly understand that the buyer has a right to the option, whereas the seller has an obligation. Because the buyer has a right, he may or may not chose to exercise that right depending upon whether he is making money or not. On the other hand, because the seller has an obligation, he will be obliged to fulfil this obligation in case the buyer exercises his right to the option. As a result of this, the buyer’s loss will be limited to the extent of premium that he has paid, while the seller’s loss will be potentially unlimited. Because the seller’s loss is potentially unlimited, a seller will need to be compensated accordingly for him to consider shorting an option. How much must the seller be compensated (in the form of a premium over the intrinsic value) depends on various factors. Here, we shall focus on just one of those factors: Volatility.
Earlier in this chapter, we saw that volatility and option price are positively correlated. In other words, higher the volatility, higher will be the option price; and lower the volatility, lower will be the option price. As volatility rises, it takes option price higher along with it; and as volatility drops, it takes option price lower along with it. Let us now explain why this happens by taking call option as an example.
Let us assume that a stock is currently trading at ₹100 and one is looking at a call option having a strike price of ₹110. As can be seen, this option is OTM by 10%. Because this option is OTM, it will have only time value and no intrinsic value. Let us assume that the price of this option is ₹5, IV is 20%, and time left to expiration is 30 days. As we saw in the previous chapter, IV is expressed in annualized terms. So, assuming there are 250 trading days in a year, the 30-day IV is 6.93% (to understand how we arrived at this figure, kindly look at the formula that we mentioned in the previous chapter). So, as per the 30-day IV, the stock could move in a range between ₹93.07 and ₹106.93 over the next 30 days. As of now, things are good for the call option seller because, based on the IV, the odds of the option expiring ITM are low. Remember, for the option to expire ITM, spot price of ₹100 will have to rise above the strike price of ₹110. This implies that the spot price should rise by at least 10% for the option to move ITM, whereas the IV is only 6.93%. So, as things stand, the call seller wouldn’t mind selling the option and receiving a premium of ₹5.
However, instead of 6.93%, what if the 30-day IV is 11.95%? Now, the price range would expand to ₹88.05 and ₹111.95. As we can now see, there is some possibility of the option going ITM by expiration. This has the potential to hurt the option seller. Hence, to sell such an option, sellers would command a higher option premium.
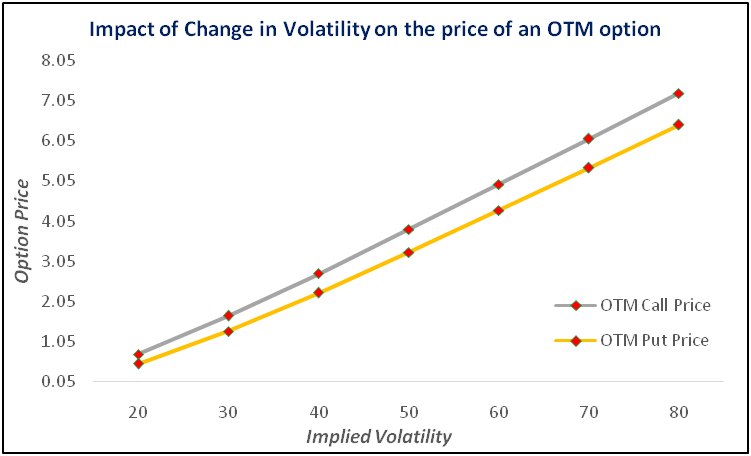
As such, when volatility goes up or is expected to go up, the price of an option also goes higher along with it. This applies not only to call options but also to put options. Similarly, when volatility goes down or is expected to go down, the price of an option also decreases. Let us now look at this from a graphical standpoint.
The chart above shows how changing volatility affects OTM option price. In the above chart, we have assumed the following:
- Underlying price = ₹100
- Strike price = ₹105 (for Call) and ₹95 (for Put)
- Time to Expiration = 30 days
- Dividend = 0
- Risk-free rate = 5%
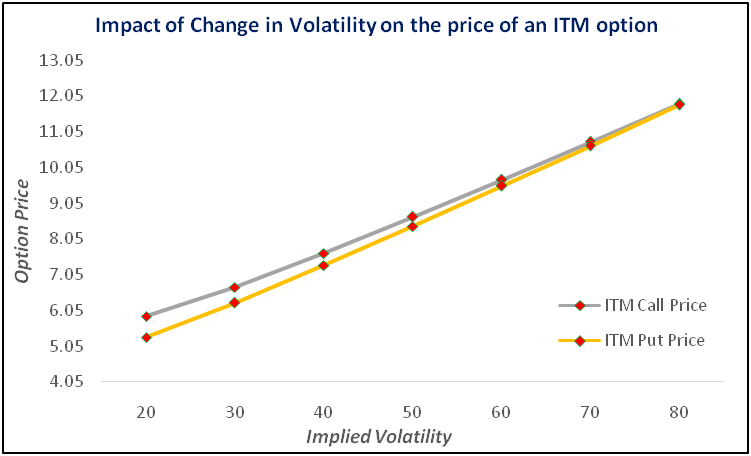
The chart above shows how changing volatility affects ITM option price. In the above chart, we have assumed the following:
- Underlying price = ₹100
- Strike price = ₹95 (for Call) and ₹105 (for Put)
- Time to Expiration = 30 days
- Dividend = 0
- Risk-free rate = 5%
Notice in both the charts that as volatility rises, so does the price of an option, be it a call option or a put option. The opposite is also true, i.e. as volatility reduces, so does the price of an option. Meanwhile, on a percentage basis, changing IVs have a greater impact on OTM options than on ITM options. For instance, in the above example, as the IV jumped 300% from 20% to 80%, the price of a call that 5% OTM rose around 900% from ₹0.73 to ₹7.23, while that of a call that is 5% ITM rose around 100% from ₹5.89 to ₹11.84. Similarly, as the IV soared 300% from 20% to 80%, the price of a put that 5% OTM rose around 1,200% from ₹0.50 to ₹6.45, while that of a put that is 5% ITM rose around 125% from ₹5.30 to ₹11.80.
Important concepts to remember about Volatility and Vega
-
Volatility is the rate at which the price of an asset fluctuates over time. An important thing to keep in mind regarding volatility is that it tells nothing about the direction in which the price of the asset is moving.
-
Standard Deviation, denoted by the Greek letter σ, measures the amount of dispersion around the mean, where mean is the average of the observations within the data set over the past ‘n’ periods.
-
Also known as statistical volatility, historical volatility measures the dispersion around the mean for daily returns on an annualized, percentage basis. It measures how volatile the movements in prices have been over the specified period.
-
Implied volatility is used to measure future volatility. It is based on what market participants imply the volatility of the underlying will be over the remaining life of an option contract.
-
Vega can be defined as the change in option price for every 1 percent change in Implied Volatility (IV). We use percentage here because Implied Volatility is expressed as a percentage.
-
The higher the implied volatility, the higher would be the change in option price, and vice versa.
-
A buyer of an option, be it a call or a put, will benefit when IVs go up and stand to lose when IVs go down. On the other hand, the seller of an option will benefit when IVs go down and suffer when IVs go up.
-
Vega is positive for long options and negative for short options. In other words, when you are long options, you tend to have a long Vega exposure. And when you are short options, you tend to have a short Vega exposure.
-
Because rising volatility works against an option seller and given how sharply it can rise in a quick span of time, short Vega positions need to be carefully monitored to ensure that their exposure are within tolerable levels.
-
Vega is identical for call and put options that have the same underlying, same expiration, and same strike price. What differs however, is the implied volatility.
-
Vega impacts only the time value component of the option price, and not the intrinsic value.
-
The higher the time to expiration of an option contract, the higher would be the Vega of the option, all else equal.
-
Vega tends to be highest for options that are ATM. As the option start moving either ITM or OTM, Vega starts declining. Vega tends to be very low in case of options that are deep ITM or deep OTM.
-
The maximum impact of change in IVs tends to occur for options that are ATM or close to being ATM because they tend to have the highest Vega.
-
The closer the probability of an option expiring ITM moves toward the extremes (i.e. 0% or 100%), the lower will the Vega be.
Next Chapter
Comments & Discussions in
FYERS Community

Knm prasad commented on January 27th, 2020 at 6:53 PM
Very good
Shriram commented on January 27th, 2020 at 8:47 PM
Thank you for the feedback sir!
Matin commented on January 28th, 2020 at 9:26 AM
Please provide in hindi modules
Shriram commented on January 28th, 2020 at 9:32 PM
Hi Matin, we are focusing on English at present as it is a lot easier to explain and understand technical-related content in English.