In this chapter, we will talk about another crucial Option Greek called Theta. We will start our discussion by introducing Theta and then talking about its other important details. We shall see why Theta is a friend to an option writer and an enemy to an option holder. Kindly go through this chapter diligently as Theta has a strong impact on the price of an option and is without a question, one of the most crucial option Greeks to keep an eye on.
Introducing Theta: A Writer’s friend, a Holder’s enemy
In an earlier chapter, we had discussed about option price (aka option premium). We had seen that option price has two elements: intrinsic value and time vale (aka extrinsic value). While intrinsic value is the ITM portion of an option, time value is the premium paid over the intrinsic value to compensate the option writer for the excess risk that he assumes when writing an option. The time value component is impacted by factors such as volatility, time left to expiration, and interest rate.
In this chapter, we shall be talking about Theta, which measures the impact of time on the price of an option. Theta is defined as a change in option price for a one unit change in the time left to expiration of an option contract. That is, Theta measures the effect of time decay on the option price. But what exactly is time decay? Time decay is the rate at which the value of an option erodes with each passing day. Keep in mind that time value is the excess premium over intrinsic value that a buyer must pay the seller to compensate him for the uncertainty or the excess risk that the seller assumes over the life of an option contract. The greater the time there is to expiration, the greater is this uncertainty. This is because more time means more room for the underlying to move. However, as the time left to expiration reduces, so does this uncertainty as the room for the underlying to move shrinks. Hence, with each passing day, the time value component of an option reduces as the risk reduces. At expiration, the time value component of an option reaches zero. The rate at which the time value component erodes with each passing day is measured by the option Greek Theta.
Theta works in favour of an option writer and against an option holder. Remember what we had said earlier, an option writer can make money even if the underlying price does not move much by expiration. However, for an option holder to make money, the underlying price must move in his favour by expiration. If this does not happen, then the option holder can suffer because time decay will cause the value of the option to erode. Because Theta works against an option holder, it is expressed as a negative number for long calls and long puts. On the other hand, because Theta works in favour of an option writer, it is expressed as a positive number for short calls and short puts. The table below highlights this for ease of reference:
| Particulars | Theta (ϴ) |
| Long Call | Negative |
| Short Call | Positive |
| Long Put | Negative |
| Short Put | Positive |
Let us now take a simple example. Let us assume a few things as follows: strike price = ₹100, underlying price = ₹100, time to expiration = 30 days, interest rate = 5%, and volatility = 20%. For a call option, Theta is -0.054, while for put option Theta is -0.041. What this essentially means is that as the number of days to expiration reduces from 30 to 29, all else constant, the theoretical value of a call option would reduce by ₹0.054 while that of a put option would reduce by ₹0.041. As we know by now, a reduction is option price hurts the option holder while benefiting the option writer. Hence, it is commonly said that Theta is an enemy to the option holder and a friend to the option writer. All else constant, the price of an option, be it a call or a put, reduces each day by the value of Theta. An interesting thing to note in this example is that the Theta of the call was higher than the Theta of the corresponding put (we will talk more about why this is the case in the next chapter). Because of this, given that at expiration the time value component of an option price reaches zero, the Theta of a call option will have to fall at a faster pace than that of a put option. Hence, all else equal, the value of a call will erode at a slightly higher pace than that of the corresponding put option.
Theta is non-linear
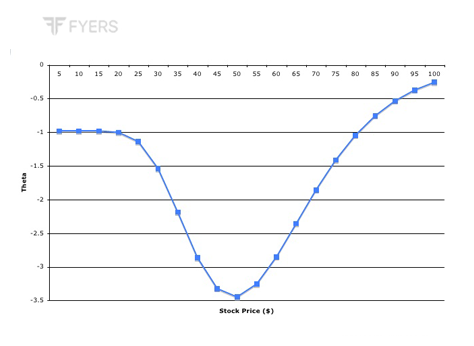
Theta for ATM options
In the above example, we saw that with 30 days left to expiration, the Theta of the call was -0.054 while that of the put was -0.041. However, as the number of days left to expiration reduces, the value of Theta also changes. In fact, for options that are ATM (which tend to have the highest Theta), Theta gets larger in absolute value terms with each passing day, before starting to rise exponentially as the expiration gets closer and closer. As an instance, for the same example above, but with just 5 days left to expiration, the Theta of a call would be -0.124 while that of a put would be -0.110. Compare and notice that with just a few days left to expiration, the absolute value of Theta increased exponentially. A very crucial thing to remember about Theta is that it is non-linear in case of ATM options, as it causes the time value component of an ATM option to reduce exponentially as the expiration gets closer. Let us try to gain more clarity about this by looking at a chart. Again, let us take the case of the ATM call option example that we presented above.
-
Strike price = ₹100
-
Spot price = ₹100
-
Time left to expiration = 30 days
-
Interest rate = 5%
-
Implied Volatility = 25%
-
Dividend = 0
In the above chart, we have assumed that the only changing variable is the time left to expiration. The rest of the four variables have remained constant throughout. We can see that the absolute value of Theta increases for an ATM call as the days left to expiration reduces. We can also observe that towards the expiry, Theta in absolute terms will get exponentially large. Because of this, all else equal, the time value component of the option price will reduce exponentially as the expiry approaches. This is a very crucial thing to note. It tells that buying an ATM option, irrespective of whether it is a call or a put, which is approaching expiry is very risky because a rapidly declining Theta will rapidly erode the time value component of the option price. Hence, unless there is a very swift and sharply favourable move in the price of the underlying, the odds of losing the premium paid are quite high for ATM options that are bought closer to expiration.
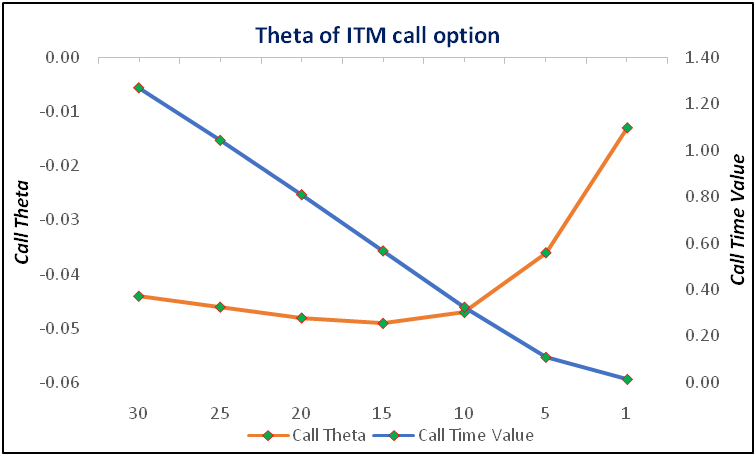
Theta for ITM options
What about an option that is ITM? Generally, for options that are ITM, the intrinsic value tends to form a larger component of the option price than the time value. Hence, because the time value is relatively less for ITM options, they tend to have a lower Theta. Also, because ITM options (especially the ones that are deep ITM) have little to lose in terms of time value, the absolute value of their Theta tends to only increase at a slower rate, before starting to fall sharply and towards zero as the expiration gets very close. Let us try to understand this using a graph. We will use the same statistics that we used in the example above, with just one change: the exercise price is ₹95.
In the above example, notice that the absolute value of Theta rose very slowly, before starting to fall exponentially as the expiration got closer. The reason why this happens is because, as stated, options that are well ITM have very low time value. By the time these options inch closer towards expiration, their time values would have reached close to zero, causing their absolute Theta to fall sharply as there is no time premium to erode.Options that are deep ITM are less sensitive to Theta, because they have less time value and more intrinsic value. Hence, they are not as much impacted by time decay as ATM options are. Given that deep ITM options have little time value in them as compared to the intrinsic value that they possess, such options can be considered for going long, especially when the objective is to have a low exposure to Theta.
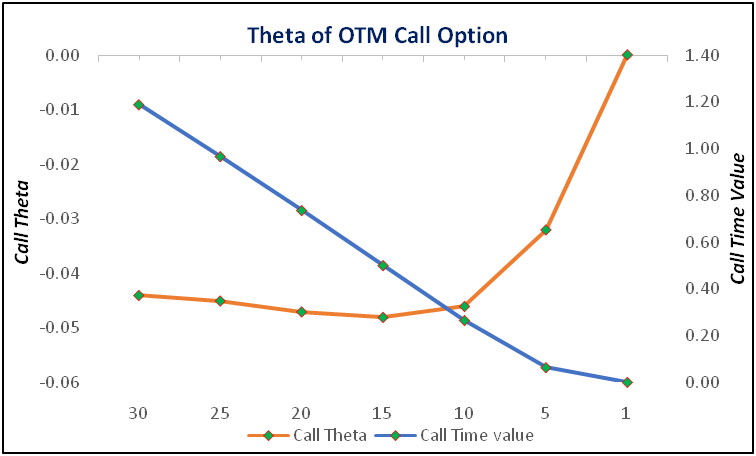
Theta for OTM options
Finally, what about an option that is OTM? Again, options that are OTM have only time value and no intrinsic value. These options, especially ones that are deep OTM, tend to have lower time values because the probability of them expiring ITM are low. The deeper an option is OTM, the lower would be their time value. Hence, because the time value is less for OTM options, they tend to have a lower Theta. Also, because OTM options have less time value, the absolute value of their Theta tends to increase at a slower rate, before falling exponentially and towards zero as the expiration gets very close. Let us try to understand this using a graph. We will use the same statistics that we used in the example above, with just one change: the exercise price is ₹105.
In the above example, notice that the absolute value of Theta rose very slowly initially, before starting to fall exponentially as the expiration drew nearer. The reason why this happens is because, as stated, options that are well OTM have very low time valueas the odds of them expiring ITM are remote. By the time these options inch closer towards expiration, their time values would have reached close to zero, causing their absolute Theta to fall sharply. Options that are deep OTM are less sensitive to Theta, because they have less time value. Hence, they are not as much impacted by time decay as ATM options are. However, they have less time value (and subsequently less Theta) for a reason, which is that the probability of them expiring ITM is low (as they have an absolute Delta of less than 0.5).
If you find this difficult to remember, keep in mind that the higher the time value component of an option price, the higher the Theta, and vice versa. Because ATM options have the highest time value, they also have the highest Theta. On the other hand, options that are ITM or OTM have lower time value in them, and hence they will have lower Theta. However, ITM and OTM options have lower time value for differing reasons. While ITM options have lower time value because they have a relatively large intrinsic value, OTM options have lower time value because they have a low likelihood of expiring ITM. Also remember that in the initial life of an option, the rate of time decay will be slow, However, as the option approaches its expiration, the time decay will acceleratebefore the time value component reaches zero at expiration.
Impact of Volatility on Theta
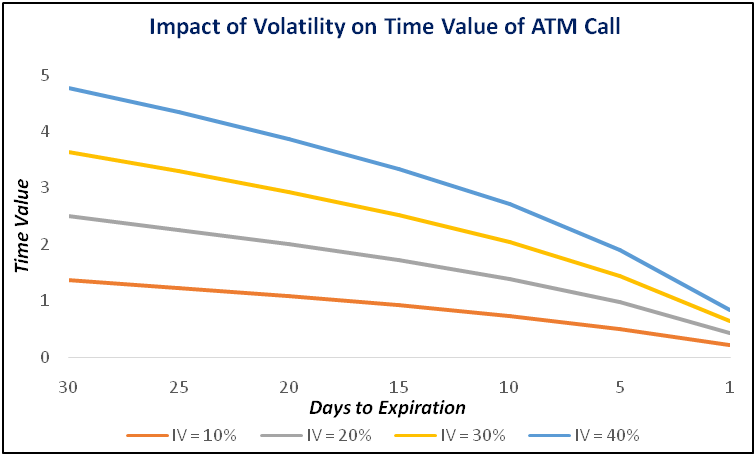
Theta is not only impacted by option moneyness but is also impacted by volatility. In this section, we shall see how volatility affects Theta. Generally, as we saw in the previous chapter, the higher the volatility, the higher would be the time value of an option and subsequently the option price. And as we know by now, the higher the time value of an option, the higher would be the Theta. The opposite is also equally true - the lower the volatility, the lower will be the time value and subsequently the Theta. So, as we can see, there is a direct correlation between volatility and Theta. Let us now try to understand how volatility impacts Theta and time value of options. For our example, we have made the following assumptions:
-
Strike price = ₹100
-
Stock price = ₹100
-
Time to expiation = 30 days
-
Implied Volatility = varies from 10% to 40%
-
Interest rate = 5%
-
Dividend = 0
Notice in the above chart that options with high volatility have high Theta values. Naturally, given this, the fall in time value for options with high volatility tends to be greater than the fall in time value for options with low volatility. It can be seen in the chart that the decline in time value is gradual initially, before accelerating towards the end of an option’s life. For instance, observe that in case of the option that has an IV of 40% and time to expiration of 30 days, half of the time value is lost during the final 7-8 days of the option’s life. It can also be noticed that for options with low volatility, the fall in time value is steadier as compared to options with high volatility, whose fall in time value tends to be steeper.
Important concepts to remember about Theta
-
Theta measures the impact of time on the price of an option. Theta is defined as a change in option price for a one unit change in the time left to expiration of an option contract. Theta is generally expressed in terms of option value that is lost each day as a result of time decay.
-
Time decay is the rate at which the value of an option erodes with each passing day.
-
Theta works in favour of an option writer and against an option holder.
-
Because Theta works against an option holder, it is expressed as a negative number for long calls and puts. On the other hand, because Theta works in favour of an option writer, it is expressed as a positive number for short calls and puts.
-
All else constant, the price of an option, be it a call or a put, reduces each day by the value of Theta.
-
All else equal, the value of a call will erode at a slightly higher pace than that of a corresponding put option. The reason why this happens is because of interest rate, which will be explained in the next chapter.
-
For options that are ATM (which tend to have the highest Theta), Theta gets larger in absolute value terms with each passing day, before starting to rise exponentially as the expiration gets closer and closer.
-
Buying an ATM option, irrespective of whether it is call or put, which is approaching expiry is very risky because a rapidly declining Theta will rapidly erode the time value of the option. Hence, unless there is a very swift and sharply favourable move in the price of the underlying, the odds of losing the premium paid are quite high for ATM options that are bought closer to expiration.
-
For options that are ITM, the intrinsic value tends to form a larger component of the option price than the time value.
-
Because the time value is relatively less for ITM options, then tend to have a lower Theta. Also, because ITM options (especially the ones that are deep ITM) have little to lose in terms of time value, the absolute value of their Theta tends to increase at a slower rate, before starting to fall sharply as the expiration gets very close.
-
Given that deep ITM options have little time value in them as compared to the intrinsic value that they possess, such options can be considered for going long, especially when the objective is to have a lower Theta exposure.
-
Options that are OTM have only time value and no intrinsic value. These options, especially ones that are deep OTM, tend to have lower time values because the probability of them expiring ITM are low.
-
The deeper an option is OTM, the lower would be their time value. Hence, because the time value is less for OTM options, then tend to have a lower Theta. Also, because OTM options have less time value, the absolute value of their Theta tends to increase at a slower rate, before falling exponentially as the expiration gets very close.
-
The higher the volatility, the higher would be the time value of an option and subsequently the option price. And the higher the time value of an option, the higher would be the Theta.
-
The opposite is also equally true - the lower the volatility, the lower will be the time value and subsequently the Theta.
-
The fall in time value for options with high volatility tends to be greater than the fall in time value for options with low volatility.
-
For options with low volatility, the fall in time value is steadier as compared to options with high volatility, whose fall in time value tends to be steeper.
Next Chapter
Comments & Discussions in
FYERS Community
Abhishek Sharma commented on August 17th, 2020 at 12:14 AM
This is the best content I have read and found on net for long long time, ZERODHA varsity is edge better , but yours is outstanding as well!
Abhishek Chinchalkar commented on August 17th, 2020 at 8:21 AM
Hi Abhishek, thank you for your valuable feedback!