In this chapter, we will talk about the last of the five Greeks: Rho. Rho is the least important option Greek, simply because it has the lowest impact on options, especially the ones that are short-term in nature. That said, we will still talk about this Greek given that it can influence the trajectory of longer-term options. So, without any further ado, let us get started on discussing about Rho.
Introducing Rho
So far, we have talked about four Greeks. These include Delta, Gamma, Vega, and Theta. Briefly recapping each of these, Delta measures the impact of change in underlying price on option price, Gamma measures the impact of change in underlying price on Delta, Vega measures the impact of volatility on option price, and Theta measures the impact of time decay on option price. Rho, meanwhile, measures the impact of changes in interest rates on option prices. Specifically, Rho measures how much impact a 1% change in interest rate has on the price of an option. So, for instance, a Rho of 0.05 on a call option means that a 1% increase in interest rate will cause the value of the call to increase by 5 paise.
A common question that could arise is, which interest rates are used in the option pricing model? The answer is the risk-free rate of return, i.e. the return earned on the nation’s sovereign instruments, such as treasuries and government securities. These are considered the safest investments out there, and hence are considered risk-free. For investments other than these, investors would expect to earn a return in excess of the risk-free rate to compensate for the additional risk that they are taking when investing in other instruments.
Earlier, we said that Rho is the least important of the five option Greeks. One reason for this is that interest rate changes are quite infrequent. Central banks usually alter their interest rates only if warranted. Otherwise, interest rates usually remain unchanged. Also, whenever central banks change interest rates, it is in smaller proportions, usually in multiples of 25 basis points (0.25%). It is very unlikely for central banks to change interest rates in larger magnitudes. Because of these, interest rates do not have a material impact on option prices. This is especially true in case of shorter-dated options, such as those having tenure of less than 3-months. The exception, however, are longer-dated options, such as the ones having tenure of one year or more. Such options are sensitive to interest rate changes.
From the context of options that are traded on Indian exchanges, given that they usually have tenures of a month or less, interest rate is not as important a factor as volatility, time to expiration, and underlying prices are.
Rho for Calls and Puts
Impact of interest rates on call options
All else constant, a rise in interest rates tends to have a positive impact on the value of a call option. The reason why this happens is because as interest rates go up, so does the opportunity cost of buying the underlying on an outright basis. Instead, buying call options on the underlying becomes more lucrative, given that options cost only a fraction of the underlying. The money that is thus saved as a result of a buying call option can then be utilized to invest in risk-free interest bearing instruments, a choice that becomes lucrative during times when interest rates increase. As a result, when interest rates go up or are expected to go up, the value of a call option tends to increase because of a potential increase in demand for them. This is even more true in case of call options that have a Delta close to 1, as they tend to move more or less as much as the underlying moves, thereby generating returns that are similar to those generated by the underlying. Apart from this, rising interest rates also benefit call options because the borrowing costs go up, making buying the underlying on borrowed money more expensive, and thereby increasing the allure to buy call options.
Let us try to understand this concept using an example. Let us assume that a stock is trading at ₹100 and a call option on this stock having a strike price of ₹95 with two months to expiration is trading at ₹8. Given this option is well ITM, it will have a Delta closer to 1. Let us assume that the Delta is 0.85. Let us also assume that the lot size is 200 shares, meaning that the total investment needed to buy this option is ₹1,600 (₹8 * 200). As we can see, a trader would have two choices in front of him. Buy the call option with a total cash outlay of ₹1,600. Or buy 200 shares outright at a total outlay of ₹20,000. If the trader choses the first option, which is buying the call, he will be saving ₹18,400 (₹20,000 - ₹1,600), which he can then utilise to invest in a risk-free instrument that would earn him a risk-free return. The higher the interest rate, the more appealing this option will become. Keep in mind that the trader wouldn’t be compromising much on returns, given that the option has a Delta near 1, which would replicate the movement in stock price.
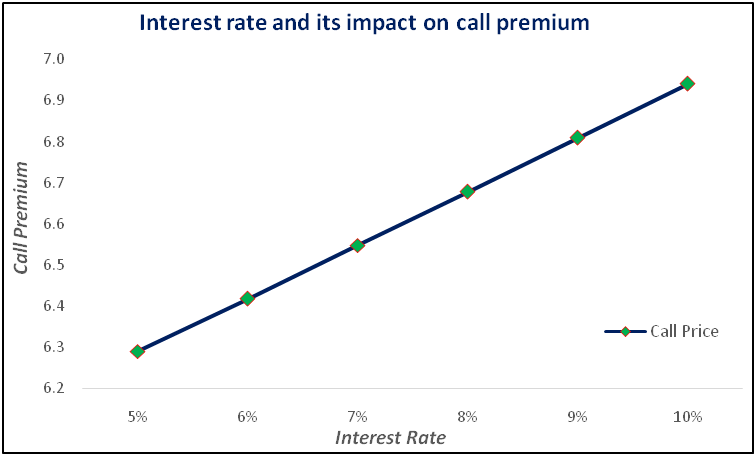
While rising interest rate has a positive impact on the value of a call option, falling interest rate has a negative impact. So, remember that interest rates and call option premiums are positively correlated. Let us understand this from a graphical standpoint. For our example, we have assumed the following:
-
Spot price = ₹100
-
Exercise price = ₹95
-
Days left to expiration = 60
-
Interest rate = varies from 5% to 10%
-
Volatility = 15%
Whichever way one looks at the above chart, notice that there is a positive correlation between interest rate and call option premium. Notice that as interest rates rose from 5% to 10%, the call option premium moved higher from ₹6.29 to ₹6.94, all else constant. However, it can also be seen that the impact of interest rate change on call option premium is not much. For instance, notice that a doubling of interest rate lifted call premium merely by 10%. What’s important to note is that interest rates don’t change by this big a magnitude in a short-span of time. In fact, it might take a year’s time for interest rates to move by a full percentage point. Because of all these reasons, traders usually do not pay much attention to Rho. Factors such as volatility and movement in the underlying price tend to have a far greater impact on option price than interest rates do.
Impact of interest rates on put options
Because rising interest rates benefit call option premiums, it is not difficult to imagine that they would hurt put option premiums. This is because during times when interest rates are rising, a trader can short sell the underlying. Doing so would lead to cash inflow into the trading account, which a trader can then utilise to invest in risk-free securities. This option can become more attractive during times when interest rates are either going up or are expected to go up. Buying a put option, on the other hand, would lead to cash outflow from the trading account rather than inflow (because you need to pay the total cost of the option when buying one). Hence, there is an opportunity loss in buying put options during times when rates are going higher. As a result, when interest rates are trending higher, put options on the underlying become relatively less attractive than short selling the underlying. Hence, the value of a put option tends to go down because of a potential reduction in demand for them.
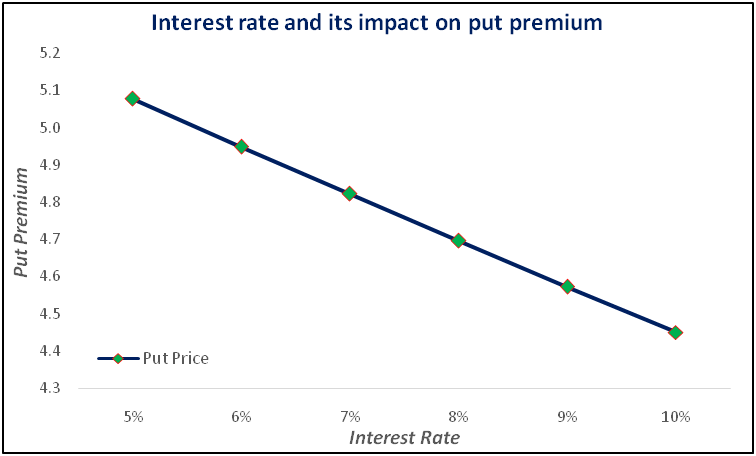
On the other hand, falling interest rates benefit put option premiums. This is because when interest rates fall, short selling the underlying becomes less attractive as the funds received from the short sale would earn lower returns if invested in risk-free instruments.Hence, on a relative basis, puts become more attractive. So, remember that interest rates and put option premiums are negatively correlated. Let us look at this from a graphical standpoint. For our example, we have assumed the following:
-
Spot price = ₹100
-
Exercise price = ₹105
-
Days left to expiration = 60
-
Interest rate = varies from 5% to 10%
-
Volatility = 15%
Notice in the graph that interest rates and put option premiums are negatively correlated. Observe that as interest rates rose from 5% to 10%, the put option premium moved lower from ₹5.07 to ₹4.45, all else constant.
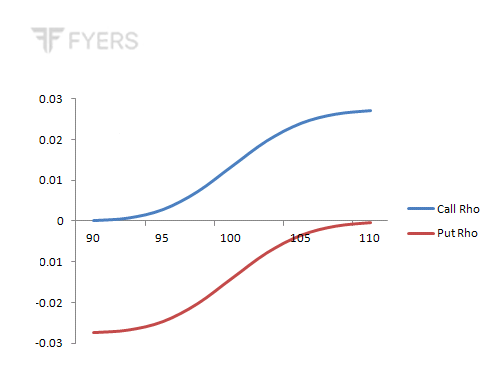
Because call options tend to gain in value when interest rates go up while put options tend to lose value when interest rates rise, Rho is positive for call options and negative for put options. This has been highlighted below for ease of reference.
| Particulars | Rho |
| Long Call | Positive |
| Short Call | Negative |
| Long Put | Negative |
| Short Put | Positive |
Because Rho is positive for calls, the buyer of a call option would want the interest rates to go higher as this would help his long call position. Similarly, because Rho is negative for puts, the buyer of a put option would want the interest rates to go down as this would help his long put position.
Impact of time on Rho
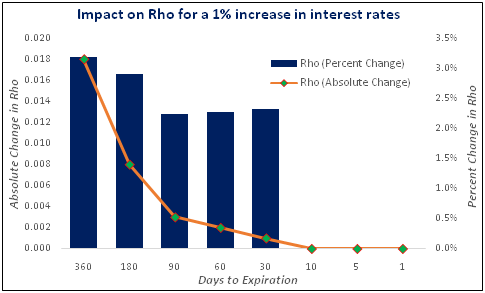
As we said earlier, options that have a long time to expiration have higher Rho values, whereas those that have a short time to expiration have lower Rho values. Because options that have a long time to expiration have higher Rho values, the impact of interest rate changes on such options is higher. Hence, traders who have positions in longer-dated options need to take interest rates into consideration as changes in rates can have an impact on option price. Similarly, because options that have a short time to expiration have lower Rho values, the impact of changes in interest rate on such options is lower. Hence, traders who are holding positions in shorter-dated options need not worry much about interest rates, as long as there is no major unexpected change in rates over the life of the option.
Let us now see this from a graphical standpoint. For our example, we have assumed the following:
-
Spot price = ₹100
-
Exercise price = ₹100
-
Days left to expiration = varies from 1 day to 360 days
-
Interest rate = increases from 5% to 6%
-
Volatility = 15%
In the above chart, the left axis shows the absolute change in Rho (represented by the orange line) and the right axis shows the percent change in Rho (represented by the blue bars). Notice how a 1% increase in interest rate impacts Rho, in both absolute terms and percentage terms. Observe that the impact of interest rate change on Rho is high when there is greater time left in an option’s life, and vice versa. As we can see in the graph, the impact of interest rate change, once the option has less than 30 days left to expiration, tends to be very small, or rather should I say negligible. For instance, notice in the above example that, despite a full percentage increase in interest rates from 5% to 6%, there was no impact on Rho at all when the number of days left to expiration was 10 and below.
A thing to keep in mind is that, in the real world, interest rates usually change in smaller proportions, typically in multiplies of 25 basis points (0.25%). Also, such changes don’t occur every day, but rather infrequently and only when warranted. As a result, options that have less time to expiration are not impacted meaningfully by changes in interest rates.
Impact of option moneyness on Rho
Whether an option is ITM, ATM, or OTM has an impact on Rho and subsequently on option price. Let us see how this happens from a graphical standpoint. For our example below, we have assumed the following:
-
Spot price = ₹100
-
Exercise price = varies from ₹85 to ₹115 in multiples of ₹3
-
Days left to expiration = 90
-
Interest rate = 5%
-
Volatility = 15%
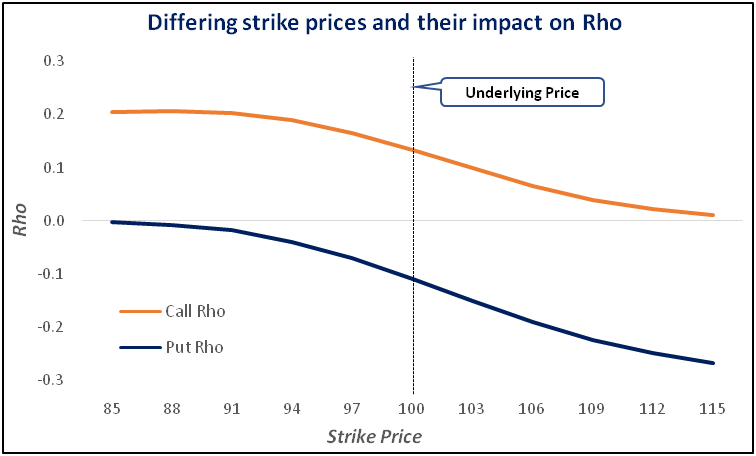
Notice in the above chart that deep ITM options have high Rho values in absolute terms. For instance, observe the Rho value for a call option that has a strike price of 85 and a put option that has a strike price of 115. Each of these has high Rho values (in absolute terms). On the other hand, OTM options have low Rho values relative to ATM and ITM options. The deeper the option is OTM, the closer will Rho values get towards zero. Options that are deep OTM can have Rho values of zero, meaning that changes in interest rate will have no impact on the price of such options.
In the above example, we saw how Rho is impacted by differing strike prices. However, what happens when the underlying price changes? An important thing to keep in mind is that even movements in the underlying price has an impact on Rho. Remember that an increase in the price of the underlying asset increases the cost of financing that asset. As a result, the Rho for both calls and putswill go up when the underlying price increases. Subsequently, this will cause the value of callsto go up and that of puts to go down. Meanwhile, the opposite is also true when the underlying price decreases.
-
Spot price = varies from ₹85 to ₹115 in multiples of ₹3
-
Exercise price = ₹100
-
Days left to expiration = 90
-
Interest rate = 5%
-
Volatility = 15%
Notice above that when the underlying price increases, so does the Rho for both calls and puts. This in turn makes calls more expensive to buy and puts less expensive to buy.
Important concepts to remember about Rho
-
Rho measures the impact of changes in interest rates on option prices. Specifically, Rho measures how much impact a 1% change in interest rate has on the price of an option.
-
Rho is the least important of the five option Greeks because interest rate changes are quite infrequent. That said, longer-dated options, such as the ones having tenure of one year or more, are sensitive to changes in interest rate. Hence, they are impacted by Rho.
-
From the context of options that are traded on Indian exchanges, given that they usually have tenures of a month or less, interest rate is not as important a factor as volatility, time to expiration, and underlying prices are.
-
All else constant, a rise in interest rates tends to have a positive impact on the value of a call option, while a fall in interest rates tends to have a negative impact. So, remember that interest rates and call option premiums are positively correlated.
-
All else constant, a rise in interest rates tends to have a negative impact on the value of a put option, while a fall in interest rates tends to have a positive impact. So, remember that interest rates and put option premiums are inversely correlated.
-
Because call options tend to gain in value when interest rates go up while put options tend to lose value when interest rates rise, Rho is positive for call options and negative for put options. However, when shorting an option, Rho is negative for calls and positive for puts.
-
Options that have a long time to expiration have higher Rho values, whereas those that have a short time to expiration have lower Rho values.
-
Deep ITM options have high Rho values in absolute terms. OTM options have low Rho values relative to ATM and ITM options.
-
Remember that an increase in the price of the underlying asset increases the cost of financing that asset. As a result, the Rho for both calls and puts will go up when the underlying price increases. Meanwhile, the opposite is also true when the underlying price decreases.
Next Chapter
Comments & Discussions in
FYERS Community

Alda commented on November 4th, 2022 at 1:12 PM
เว็บตรง ค่าย pgมาแรงจนฉุดไม่อยู่ เล่นง่าย จ่ายทุกบิล ทำเทิร์นน้อยสำหรับโบนัส และ โปรโมชั่นที่ท่านเลือก ได้รับการส่งเสริมจากเว็บ pgslotgame.vip ที่เปิดให้บริการPGSLOTมานานกว่า 3 ปี เหมาะกับผู้เล่นทุกระดับ ไม่ว่าจะเป็นผู้เล่น ทุนน้อย ทุนหนัก ก็สามารถเล่นได้
มีพนักงานรอดูแลท่าน ตลอด 24 ชั่วโมง พร้อมระบบฝากถอนออโต้ใช้งานง่ายไม่ต้องโหลดappสามารถเข้าเล่นผ่านหน้าเว็บได้ในทันที มีผู้เล่นมากมายก่ายกองจากทั่วทุกประเทศในโลก ลงทะเบียนกับเราวันนี้ รับโบนัสฟรี 100% ยิ่งกว่านั้นยังมีการแจกวิธีการเล่นสล็อตออนไลน์ฟรีๆทุกวัน รวมเกมส์PG
SLOT AUTOตื่นเต้นตื่นเต้นไม่ว่าจะเป็นเกมส์สล็อตเล่นง่ายหรือกีฬาฟุตบอลจากลีกชั้นหนึ่งทั้งโลก
รวมทั้งรวมถึงฟุตบอลรายการต่างๆเยอะมาก ที่เปิดให้คุณมาเพลินใจมากกว่าทุกที่ เปิดประสบการณ์ที่บันเทิงใจที่สุด ได้กำไรมากที่สุด เพราะเราเป็นสล็อต เว็บตรง
แตกง่ายที่ดีที่สุดในไทย ยืนยันเรื่องของการจ่ายเงินแน่ๆ เพราะว่าเว็บของเรานั้นมีความยั่งยืนและมั่นคงแล้วก็ปลอดภัย100% สล็อตเว็บตรง
Roscoe commented on January 20th, 2023 at 6:06 PM
เว็บพนันslot ของทาง GODBET789 เป็น หนึ่งในผู้ให้บริการslot online
เว็บตรงที่มีความปลอดภัยสูง เรามีความยั่งยืนและมั่นคงในเรื่องเกี่ยวกับการเงิน ไม่มีปิดหนี้ ไม่มีการฉ้อฉลเงินและไม่มีประวัติการฉ้อฉลเงินแม้กระทั้งครั้งเดียว ผู้เล่นทุกคนสามารถเล่นสล็อตเว็บตรง ได้เงินจริงอย่างแน่นอน 100% พวกเรามีเกมslot online เว็บตรงให้เลือกเล่นล้นหลามกว่า 29 ค่าย ไม่ว่าจะเป็น พีจีสล็อต, สล็อต
xo, JOKERSLOT, superslot, สล็อต amb, pragmatic plays แล้วก็ค่ายอื่นๆอีกมาก
รวมแล้วพวกเรามีเกมslot เว็บตรงให้เล่นมากยิ่งกว่า 1,000 เกมส์ 1,000 แบบสำหรับในการเล่น ด้วยเว็บไซต์ของเรานั้นเป็น เว็บตรงไม่ผ่านเอเย่นต์ ทำให้สมาชิกจะได้เล่นสล็อตออนไลน์กับทางบริษัทผู้ผลิตเกมส์โดยตรง ตัวเกมslot
online เว็บตรงของพวกเรานั้นจะไม่มีการปรับปรุงแก้ไขดัดแปลงตัวเกมส์และไม่ปรับเปลี่ยนอัตราการจ่ายเงินอย่างแน่นอน ผู้เล่นจะได้สัมผัสถึงเกมSLOT เว็บตรง แตกหนัก และก็มีรางวัลแจ็คพอตในทุกตัวเกมส์ ทางเราได้คัดสรรค์ เกมสล็อตออนไลน์ ที่เป็นสล็อตวีดีโอ 3 มิติมาใหม่ ภาพสวยกราฟฟิคแน่นๆทั้งยังมีฟีเจอร์ต่างๆไม่ว่าจะเป็น Freespin, Freegame, Wild ที่ช่วยทำให้ผู้เล่นได้เงินรางวัลที่มากมายแล้วก็ง่ายดายมากยิ่งขึ้นอีก
ท่านจะได้รับประสบการณ์การเล่นSLOTแบบใหม่ที่สนุกสนานรวมทั้งทำเงินออกมาใช้จ่ายได้อีกด้วย นักลงทุนสามารถเล่นสล็อตออนไลน์เว็บตรง ได้บนคอมพิวเตอร์และโทรศัพท์เคลื่อนที่ รองรับแพลตฟอร์ม ไอโอเอส และ Android สามารถคว้าเงินรางวัลกับทางพวกเราได้ทุกที่ทุกเวลาไม่ว่าจะอยู่ไหนของมุมโลก เริ่มเดิมพัน BET กับทางเราได้ตั้งแต่หลักหน่วยไปจนกระทั่งหลักพัน รวมทั้งยังสามารถคว้าเงินรางวัลหลักพันถึงหลักล้านได้อย่างยิ่งจริงๆ ทางเว็บเว็บตรงสล็อตออนไลน์ของเรานั้นสามารถทำรายการฝากถอนได้แบบไม่มีขั้นต่ำ ซึ่งเริ่มต้นที่ 1 บาทเพียงเท่านั้น สามารถทำรายการได้ตลอด 24 ชั่วโมง ไม่กำจัดปริมาณครั้งสำหรับการฝากถอน และด้วยระบบฝากถอนออโต้ของทางพวกเรา ผู้เล่นสามารถทำรายการฝากถอนได้ด้วยตัวเอง ไม่จำเป็นที่ต้องส่งสลิปให้ adminให้เสียเวล่ำเวลา เพียงโอนเงินเข้าต่อจากนั้นรอคอยเงินเข้าเพียงเท่านั้น ไม่จำเป็นที่จะต้องโอนเงินเป็นปริมาณเศษ โอนเท่าที่ต้องการเล่น ใช้เวลาสำหรับการฝากถอนเพียงแต่ 15 วินาทีเท่านั้น เว็บไซต์slotของพวกเราเปิดให้บริการฝากถอนทุกธนาคารของประเทศไทย ทำธุรกรรมได้อย่างไม่ต้องเสียค่าบริการ และก็สำหรับผู้ที่ไม่มีบัญชีธนาคารแต่ต้องการเล่นเกมสล็อตออนไลน์เว็บตรงกับทางเรา สามารถฝากถอนผ่านทรูวอเลท (True Wallet) ได้โดยไม่ต้องมีบัญชีธนาคาร เว็บไซต์สล็อตออนไลน์เว็บตรงของเรานั้นมิได้เปิดให้บริการเดิมพันแค่เพียงเกมสล็อตออนไลน์เพียงอย่างเดียว ทางเรานั้นยังเป็นคาสิโนแบบครบวงจร ที่มีให้เลือกเล่น ฺBaccarat, เดิมพันฟุตบอล,
สลากกินแบ่ง, ไฮโล, Roulette, เกมยิงปลาและก็อื่นๆอีกมากมาย เว็บไซต์พนันออนไลน์เว็บตรงตรงของเรานั้นได้นำคาสิโนค่ายต่างที่ได้มาตราฐานมาให้นักพนันได้เล่น ไลฟ์สดและเดิมพันกันได้อย่างเรียลไทม์ ร่วมบันเทิงใจกับทางเราได้แบบไม่มีอย่างต่ำ เว็บไซต์เว็บตรงสล็อต เว็บใหญ่ที่ได้รับความนิยมสูงที่สุดในปี
2022 มีนักพนันออนไลน์เข้ามาร่วมบันเทิงใจกับทางเราหลายประเทศทั่วโลก พวกเราเป็นสล็อตใหญ่ที่มีเครือยข่ายมากไม่น้อยเลยทีเดียว เชื่อถือเลยว่าเล่นกับพวกเราอย่างไรก็ไม่มีปิดเว็บไซต์หนี้อย่างแน่นอน เว็บสล็อตยอดฮิตที่สุดในไทย มีผู้รับบริการมากกว่า 50,000 คนต่อวัน เปิดให้บริการทุกคนได้ร่วมสนุกสนานตลอด
24 ชั่วโมง อย่างไร้ข้อจำกัด จะเล่นตอนไหนก็ได้เพียงแค่ยกมือถือขึ้นมาเพียงเท่านั้น สำหรับคนที่สนใจต้องการเล่นSLOT เว็บตรงกับทางพวกเรา จำเป็นต้องลงทะเบียนสมัครสมาชิกกับทางเราก่อน เพื่อท่านจะได้มี Username และ Password ไว้สำหรับทำล็อคอินเข้าระบบเพื่อเล่นเกมส์ รวมทั้งเอาไว้สำหรับทำฝากถอนเงินเข้าบัญชีของท่าน ซึ่งทางพวกเราจะเก็ยบข้อมูลนี้เป็นความลับไม่มีผู้ใดสามารถเข้าถึงได้ มีความปลอดภัยที่สูงด้วยเทคโนโลยีเข้ารหัสล่าสุดขณะนี้ โดยวิธีการสมัครกับทางเรานั้นมีขั้นตอนการสมัครที่ง่ายสุดๆ ไม่กี่ขั้นตอน ทั้งยังสามารถทำสมัครได้ฟรี
ไม่จำเป็นที่จะต้องโอนเงินก่อน แล้วก็สำหรับท่านที่พึงพอใจลงทะเบียนสมัครสมาชิกวันนี้ เว็บตรงสล็อต มีโปรโมชั่นที่จะให้โบนัสท่านถึง 100% ยอมรับได้ตั้งแต่ทีแรกที่สมัคร สล็อตเว็บตรง 2022 (godbet789.com)
Lucile commented on January 22nd, 2023 at 2:29 PM
เว็บสล็อตออนไลน์ ของทาง
GODBET789.COM คือ หนึ่งในผู้ให้บริการสล็อตเว็บตรงไม่ผ่านเอเย่นต์ที่มีความปลอดภัยสูง พวกเรามีความยั่งยืนและมั่นคงในเรื่องของการเงิน ไม่มีปิดหนี้ ไม่มีการคดโกงเงินและไม่มีประวัติการฉ้อฉลเงินแม้กระทั้งครั้งเดียว นักลงทุนทุกคนสามารถเล่นSLOT ONLINE เว็บตรง ได้เงินจริงอย่างแน่นอน 100% พวกเรามีเกมสล็อตเว็บตรงให้เลือกเล่นจำนวนมากกว่า 29 ค่าย ไม่ว่าจะเป็น PGSLOT, slotxo, JOKER SLOT, SUPER SLOT, SLOT AMBBET, PRAGMATIC PLAYS และค่ายอื่นๆอีกเพียบ รวมแล้วเรามีเกมslot
online เว็บตรงให้เล่นมากยิ่งกว่า 1,000 เกมส์ 1,000
แบบในการเล่น ด้วยเว็บของพวกเรานั้นเป็น เว็บตรง ทำให้สมาชิกจะได้เล่นslotกับทางบริษัทผู้ผลิตเกมส์โดยตรง ตัวเกมเว็บตรงไม่ผ่านเอเย่นต์ของเรานั้นจะไม่มีการดัดแปลงแก้ไขตัวเกมส์และไม่เปลี่ยนแปลงอัตราการจ่ายเงินอย่างแน่นอน ผู้เล่นจะได้สัมผัสถึงเกมสล็อตเว็บตรง แตกหนัก
แล้วก็มีรางวัลแจ็คพอตในทุกตัวเกมส์ ทางเราได้คัดสรรค์ SLOT ที่เป็นสล็อต3Dรูปแบบใหม่ ภาพสวยกราฟฟิกแน่นๆทั้งยังยังมีFeatureต่างๆไม่ว่าจะเป็น
Freespin, Freegame, Wild ที่ช่วยทำให้ผู้เล่นได้เงินรางวัลที่เยอะแยะและก็ง่ายดายมากยิ่งขึ้นอีก ท่านจะได้รับประสบการณ์การเล่นSLOTแบบใหม่ที่สนุกแล้วก็ทำเงินออกมาใช้จ่ายได้อีกด้วย ผู้ใช้บริการสามารถเล่นslot online เว็บตรง
ได้บนคอมพิวเตอร์และมือถือ รองรับแพลตฟอร์ม ไอโอเอส รวมทั้ง Android
สามารถคว้าเงินรางวัลกับทางเราได้ทุกที่ที่ต้องการไม่ว่าจะอยู่ตรงไหนของมุมโลก
เริ่มเดิมพัน BET กับทางเราได้ตั้งแต่หลักหน่วยไปจนกระทั่งหลักพัน และก็ยังสามารถคว้าเงินรางวัลหลักพันถึงหลักล้านได้อย่างยิ่งจริงๆ ทางเว็บไซต์เว็บตรงสล็อตออนไลน์ของพวกเรานั้นสามารถทำรายการฝากถอนได้แบบไม่มีอย่างน้อย
ซึ่งเริ่มต้นที่ 1
บาทเพียงเท่านั้น สามารถทำรายการได้ทั้งวันทั้งคืน ไม่กำจัดปริมาณครั้งในการฝากถอน และก็ด้วยระบบฝากถอนออโต้ของทางเรา ผู้เล่นสามารถทำรายการฝากถอนได้ด้วยตัวเอง ไม่จำเป็นที่จะต้องส่งสลิปให้ adminให้เสียเวล่ำเวลา เพียงโอนเงินเข้าแล้วหลังจากนั้นคอยเงินเข้าเพียงเท่านั้น ไม่มีความจำเป็นต้องโอนเงินเป็นจำนวนเศษ โอนเท่าที่ต้องการเล่น ใช้เวลาสำหรับการฝากถอนเพียงแต่ 15 วินาทีเท่านั้น เว็บslotของพวกเราเปิดให้บริการฝากถอนทุกธนาคารของประเทศไทย ทำธุรกรรมได้อย่างไม่ต้องเสียค่าธรรมเนียม และสำหรับคนที่ไม่มีบัญชีธนาคารแต่อยากเล่นเกมสล็อตเว็บตรงกับทางพวกเรา สามารถฝากถอนผ่านทรูวอเลท (True Wallet) ได้โดยไม่ต้องมีบัญชีธนาคาร เว็บไซต์SLOT ONLINE เว็บตรงของพวกเรานั้นไม่ได้เปิดให้บริการพนันเพียงแต่slot onlineเพียงอย่างเดียว ทางพวกเรานั้นยังเป็นเกมคาสิโนออนไลน์แบบครบวงจร ที่มีให้เลือกเล่น Baccarat Online, พนันกีฬา,
สลากกินแบ่ง, Sic Bo, รูเล็ต,
เกมยิงปลาแล้วก็ฯลฯ
เว็บพนันออนไลน์เว็บตรงตรงของเรานั้นได้นำคาสิโนค่ายต่างที่ได้มาตราฐานมาให้ผู้เล่นได้เล่น ไลฟ์สดและพนันกันได้อย่างเรียลไทม์ ร่วมสนุกกับทางพวกเราได้แบบไม่มีอย่างต่ำ เว็บไซต์สล็อตไม่ผ่านเอเย่นต์ เว็บตรงที่ได้รับความนิยมมากที่สุดในปี 2022 มีนักพนันออนไลน์เข้ามาร่วมบันเทิงใจกับทางเราหลายประเทศทั่วทั้งโลก พวกเราเป็นสล็อตใหญ่ที่มีเครือยข่ายจำนวนมาก
เชื่อมั่นเลยว่าเล่นกับเรายังไงก็ไม่มีปิดเว็บหนี้สินอย่างแน่แท้ เว็บสล็อตที่ได้รับความนิยมที่สุดในไทย มีผู้ใช้บริการมากกว่า 50,000 คนต่อวัน
เปิดให้บริการทุกท่านได้ร่วมบันเทิงใจตลอด 1 วัน
อย่างไร้ขีดจำกัด
จะเล่นตอนไหนก็ได้แค่เพียงยกมือถือขึ้นมาเพียงเท่านั้น สำหรับผู้ที่พึงพอใจต้องการเล่นSLOT เว็บตรงกับทางเรา จำเป็นต้องสมัครสมาชิกกับทางพวกเราก่อน เพื่อท่านจะได้มี Username และ Password ไว้สำหรับกระทำล็อคอินเข้าระบบเพื่อเล่นเกมส์ และก็เอาไว้สำหรับกระทำการฝากถอนเงินฝากบัญชีของท่าน ซึ่งทางพวกเราจะเก็ยบข้อมูลนี้เป็นความลับไม่มีใครสามารถเข้าถึงได้ มีความปลอดภัยที่สูงด้วยเทคโนโลยีเข้ารหัสปัจจุบันขณะนี้ โดยแนวทางการสมัครกับทางเรานั้นมีแนวทางการสมัครที่ง่ายสุดๆ ไม่กี่ขั้นตอน ทั้งยังยังสามารถกระทำการสมัครได้ฟรี ไม่มีความจำเป็นที่ต้องโอนเงินก่อน รวมทั้งสำหรับท่านที่พอใจลงทะเบียนสมัครสมาชิกวันนี้ SLOT ONLINE เว็บตรง มีโปรโมชั่นที่จะให้โบนัสท่านถึง 100% รับได้ตั้งแต่หนแรกที่สมัคร สล็อตเว็บตรง แตกง่าย
(godbet789.com)