In this previous chapter, we talked in detail about Delta. In this chapter, we will continue our discussion from the earlier chapter and talk about the next Option Greek:Gamma. We shall first explain what Gamma means, before proceeding to its practical application.Having good understanding of Gamma would enable one to understand how changes in the underlying price impact the Delta(i.e directional risk) of an option, which intern influences the option price. So, without any further ado, let's get started.
Understanding Gamma
In the previous chapter, we saw why Delta is so crucial in the success of an option trade. We saw that using Delta, we can roughly estimate what the new option price could be for a certain point change in the value of the underlying. However, as we highlighted at the end of the previous chapter, Delta is dynamic. In other words, as there are changes in the underlying price, time to expiration, volatility, interest rates etc., the value of Delta will also change. While Delta measure the change in option price for a change in the underlying price, the question that now arises is, is there a way to measure the change in Delta, given that Delta is not static?
Fortunately, there is. This change can be measured using the Option Greek called Gamma. As Delta is a derivative of option price, it is known as the first order derivative. Gamma, on the other hand, is the derivative of Delta. That is, Gamma is a derivative of a derivative, and hence is the second order derivative. Gamma is the rate of change in Delta for every 1 point move in the price of the underlying.While Delta measures the directional risk of an option, Gamma measures the changes in that directional risk. By understanding and tracking Gamma of options, one will know how to interpret the potential movement in Delta that could be caused by changes in the underlying price.And this is important because, depending on the value of Gamma, a trader can assess the changes in his position risk. Put it in the form of an equation, Gamma can be expressed as:
Because we are interested in calculating the potential change in the value of Delta for a one point change in the underlying price, this equation can be rephrased as:
Change in Delta = Gamma * Change in the underlying price
Where, Change in the underlying price = New underlying price - Old underlying price
From this, we can calculate the new value of Delta as:
New Delta = Old Delta + Change in Delta
To understand this, let us take a simple example. Let us assume that a stock is currently trading at ₹100 and that we are looking at an ATM call option having a strike price of ₹100. Let us also assume that at present, this call option’s Delta is 0.5, Gamma is 0.02, and Option price is ₹6.
In a few days, let’s say the stock price has risen to ₹105. Using this, we can calculate the new option price as ₹6 (Old Option price) + 0.5 (Delta) * ₹5 (Change in the underlying price). This turns out to be ₹8.5. We had already seen such a calculation in the previous chapter, so nothing new here. But, given that the underlying price has now changed and that the option has moved ITM, the Delta will also change. How do we now calculate the new Delta? The New Delta can be calculated as 0.5 (Old Delta) + 0.02 (Gamma) * 5 (Change in the underlying price). This turns out to be 0.6. So, the new Delta for a 5 point rise in the underlying is 0.6. Notice that as the option has now moved ITM, its Delta has moved above 0.5.
On the other hand, what if the stock price had instead declined to ₹95? In this case, the option price would have fallen to ₹3.5. Also, given that the underlying price has changed, there will be a change in the value of the Delta as well. This change can be calculated as 0.02 * (-5), which is -0.1. Hence, the new Delta would be 0.5 + (-0.1) = 0.4. Notice that as the option has now moved OTM, its Delta has declined below 0.5.
Note: Kindly keep in mind that in the real world, the change in the value of Delta and subsequently the option price will be slightly different than the one we have calculated above. This is because in the real world, the Delta and Gamma will keep changing as and when the underlying price, time, and volatility changes. Hence, it is complicated to calculate what the exact Delta and Option price would be when the underlying price changes from, say, ₹100 to ₹105. This is because the price will keep changing constantly until the time it reaches ₹105, causing the Gamma and Delta to change constantly as well.
Let us now look at more examples.
| Option Type | Spot Price | Strike Price | Moneyness | Option Price | Delta | Gamma |
| Call | ₹100 | ₹100 | ATM | ₹6.0 | 0.50 | 0.0200 |
| ₹105 | ITM | ₹8.5 | 0.60 | 0.0179 | ||
| ₹103 | ITM | ₹7.3 | 0.56 | 0.0190 |
| Option Type | Spot Price | Strike Price | Moneyness | Option Price | Delta | Gamma |
| Call | ₹100 | ₹100 | ATM | ₹6.0 | 0.50 | 0.0200 |
| ₹95 | OTM | ₹3.5 | 0.40 | 0.0183 | ||
| ₹102 | ITM | ₹6.3 | 0.53 | 0.0193 |
| Option Type | Spot Price | Strike Price | Moneyness | Option Price | Delta | Gamma |
| Put | ₹100 | ₹100 | ATM | ₹6.0 | -0.50 | 0.0200 |
| ₹95 | ITM | ₹8.5 | -0.60 | 0.0183 | ||
| ₹100 | ATM | ₹5.5 | -0.51 | 0.0197 |
| Option Type | Spot Price | Strike Price | Moneyness | Option Price | Delta | Gamma |
| Put | ₹100 | ₹100 | ATM | ₹6.0 | -0.50 | 0.0200 |
| ₹104 | OTM | ₹4.0 | -0.42 | 0.0186 | ||
| ₹99 | ITM | ₹6.1 | -0.51 | 0.0197 |
As we can see from the above examples, the Gamma affects the Delta, which in turn affects the Option price. Hence, it is important to not just focus on Delta, but on Gamma as well, given its indirect impact on Option price. While Delta tells about the directional risk of an option, Gamma tells about the momentum of Delta. That is, Gamma measures the speed at which Delta moves. Rising Gamma values mean that any change in the underlying price would lead to a greater change in the value of Delta, which in turn would lead to a greater change in the Option price, and vice versa.
Just like Delta, Gamma is also dynamic:
Gamma is expressed as a positive number and fluctuates in value between 0 and 1, irrespective of whether the option is a call option or a put option. The higher the value of Gamma, the higher would be the movement in Delta for a 1 point change in the value of the underlying, and vice versa. An important thing to keep in mind is that Gamma is high when the option is Near-the-Money (NTM)i.e., when the strike price and the underlying price are very close to each other. When the two start moving away from each other, the value of Gamma starts reducing. When the option is deep ITM or deep OTM, the Gamma of that option is close to zero. The chart below highlights this.
Notice from the above chart how Gamma tends to typically move. Observe that Gamma takes the shape of a bell curve - being at its peak with the underlying is close to the strike and tapering off as the two start moving away from each other. Let us now understand the logic behind Gamma’s movement. To do this, let us first recap how Delta moves. Recollect that:
-
Delta fluctuates between 0 and 1 for call options and between 0 and -1 for put options.
-
Call options that are deep ITM will have Delta close to 1.
-
Put options that are deep ITM will have Delta close to -1.
-
ATM calls will have Delta of 0.5.
-
ATM puts will have Delta of -0.5.
-
Call and put options that are deep OTM will have Delta close to 0.
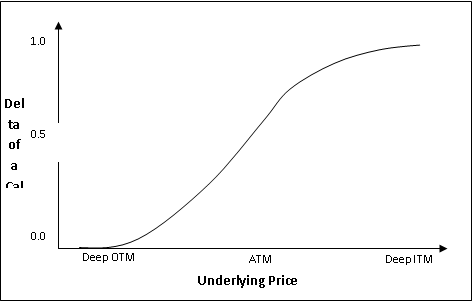
The maximum move in Delta occurs when the option is either ATM or NTM i.e. when the strike price and the underlying price are very close to each other. This is the region where the probability of an option being ITM or OTM is maximum when the underlying price changes. The above chart, which is that of a call option, would help explain this better. Notice in the chart that the slope of Delta tends to be its steepest when the call is ATM or NTM. To the extreme left, observe that Delta is 0 as the option is deep OTM. At this zone, the Delta of a call option won’t be much impacted by a small rise in the underlying price. At the other extreme, observe that Delta is 1 as the option is deep ITM. At this zone, the Delta of a call will not be much impacted by a small decline in the underlying price.
Now that we have recapped some of the key concepts pertaining to Delta, let us focus on Gamma. As already stated, Gamma will be high when the difference between the strike price and the underlying price is either zero or close to being zero. At this point, there is the highest level of uncertainty as to whether the option will be ITM or OTM by the expiration date. As the absolute value of Delta will be 0.5 at this point, it will have the highest room to move either towards 0 or 1, depending upon how the underlying pricemoves. And as the Delta will have the highest room to change at this point, it naturally follows that Gamma would need to be at its peak for this to happen.
On the other hand, as the strike price and the underlying price start deviating from each other i.e. as the option starts moving further ITM or OTM, the Gamma will start tapering off. The reason why this happens is because there is a lower and upper limit to Delta. As we know, the absolute value of Delta has an upper limit of 1. As an ITM option moves further ITM, the speed at which the Delta is rising will eventually slowdown. In other words, the Gamma will become smaller and smaller. Keep in mind that when the absolute value of Delta has reached 1 (occurs when the option has moved deep ITM), it cannot rise any further. This can only happen when the Gamma has reached 0. Hence, when the absolute value of Delta has reached 1, the Gamma would have reached 0. Similarly, as an OTM option moves further OTM, the speed at which the Delta is falling will eventually slowdown. That is, the Gamma will become smaller and smaller. Keep in mind that when the absolute value of Delta has reached 0 (occurs when the option has moved deep OTM), it will stop reducing any further. Thiscan only occur when the Gamma has also reached 0. Hence, when the absolute value of Delta has reached 0, the Gamma would have reached 0.
Let us now summarize the relation between Delta and Gamma in a tabular format before proceeding to the next section:
| Particulars | Delta | Gamma |
| Keep in mind | Measures the rate of change in option price, or the probability of an option expiring ITM | Measures the rate of change in Delta, or the speed at which Delta is accelerating |
| When an option is ATM or NTM | ±0.5 | Usually at its peak value |
| As an option starts moving away from being ATM | Can move towards ±1 or towards 0 | Decreases |
| When an option is deep ITM | Close to ±1 | Close to 0 |
| When an option is deep OTM | Close to 0 | Close to 0 |
| Call option range | 0 to 1 | 0 to 1 |
| Put option range | 0 to -1 | 0 to 1 |
Positive Gamma vs. Negative Gamma
We have seen that Gamma is positive for both call and put options. This statement is true for an option buyer. In other words, when a person buys an option, irrespective of whether it is a call option or a put option, the Gamma is positive, and the buyer is said to be long the Gamma. Positive Gamma causes the Delta of a long option position to move towards 1 when the underlying price rises (in case of a call) or towards -1 when it drops (in case of a put). Similarly,positive Gamma causes the Delta of a long option position to move towards 0 when the underlying price falls (in case of a call) or rises (in case of a put). Let us understand this using a few examples.
| Option Type | Strike Price | Spot Price | Option Price | Delta | Gamma |
| Call (Long) | ₹100 | ₹100 | ₹6.00 | 0.500 | 0.055 |
| ₹101 | ₹6.50 | 0.555 | 0.052 | ||
| ₹102 | ₹7.06 | 0.607 | 0.048 | ||
| ₹103 | ₹7.66 | 0.655 | 0.042 | ||
| ₹104 | ₹8.32 | 0.697 | 0.036 |
| Option Type | Strike Price | Spot Price | Option Price | Delta | Gamma |
| Call (Long) | ₹100 | ₹100 | ₹6.00 | 0.500 | 0.055 |
| ₹99 | ₹5.50 | 0.445 | 0.052 | ||
| ₹98 | ₹5.06 | 0.393 | 0.048 | ||
| ₹97 | ₹4.66 | 0.345 | 0.042 | ||
| ₹96 | ₹4.32 | 0.303 | 0.036 |
In the above example, two cases are presented. The case on the top shows the underlying price rising, while the one below it shows the underlying price declining. Option type in both the cases is a call option. Notice that as the underlying has increased from ₹100 to ₹104 (a price gain of ₹4), the price of the call option has moved higher from ₹6.00 to ₹8.32, which is a price gain of ₹2.32. On the other hand, notice that as the underlying has decreased from ₹100 to ₹96 (a price decline of ₹4), the price of the call option has slipped from ₹6.00 to ₹4.32, which is a price decline of ₹1.68. Notice the difference? When the underlying price rose, the call option price appreciated in value more than when the underlying price fell by the same magnitude. The reason why this happens is because of the impact of positive Gamma. In other words, because the Gamma is a positive number and because the underlying price is moving higher, it causes the Delta to become larger in absolute value terms, thereby causing the call option price to increase by a larger magnitude. On the other hand, when the underlying price is moving lower, it causes the Delta to become smaller in absolute value terms, thereby causing the call option price to decrease by a smaller magnitude.
Put options also behave in a similar fashion. Let us look at how this happens in the table below.
| Option Type | Strike Price | Spot Price | Option Price | Delta | Gamma |
| Put (Long) | ₹100 | ₹100 | ₹6.00 | -0.500 | 0.055 |
| ₹99 | ₹6.50 | -0.555 | 0.052 | ||
| ₹98 | ₹7.06 | -0.607 | 0.048 | ||
| ₹97 | ₹7.66 | -0.655 | 0.042 | ||
| ₹96 | ₹8.32 | -0.697 | 0.036 |
| Option Type | Strike Price | Spot Price | Option Price | Delta | Gamma |
| Put (Long) | ₹100 | ₹100 | ₹6.00 | -0.500 | 0.055 |
| ₹101 | ₹5.50 | -0.445 | 0.052 | ||
| ₹102 | ₹5.06 | -0.393 | 0.048 | ||
| ₹103 | ₹4.66 | -0.345 | 0.042 | ||
| ₹104 | ₹4.32 | -0.303 | 0.036 |
The table above presents the example of a put option. Notice that as the underlying decreased from ₹100 to ₹96 (a price drop of ₹4), the price of the put option moved higher from ₹6.00 to ₹8.32, which is a price gain of ₹2.32. On the other hand, notice that as the underlying increased from ₹100 to ₹104 (a price gain of ₹4), the price of the put option slipped from ₹6.00 to ₹4.32, which is a price decline of ₹1.68. Notice the difference? When the underlying price fell, the put option price appreciated in value more than when the underlying price rose by the same magnitude. Again, this happens because of the impact of positive Gamma. In other words, because the Gamma is a positive number and because the underlying price is moving lower, it causes the Delta to become larger in terms of absolute value, thereby causing the put option price to increase by a larger magnitude. On the other hand, when the underlying price is moving higher, it causes the Delta to become smaller in terms of absolute value, thereby causing the put option price to decrease by a smaller magnitude.
Meanwhile, because positive Gamma works in favour of an option holder, it is logical to think that it works against the option writer. When a person sells an option, the Gamma is negative, and the seller is said to be short the Gamma. Short Gamma causes the call Delta to decrease and move towards -1 when the underlying price rises. On the other hand, short Gamma causes the call Delta to increase and move towards 0 when the underlying price drops. Similarly, short Gamma causes the put Delta to increaseand move towards 1 when the underlying price falls. On the other hand, short Gamma causes the put Delta to decrease and move towards 0 when the underlying price rises.When a person is short the Gamma, he would want the underlying to remain more or less stable. Sharp adverse movements against the direction of the short position would aggravate the losses of the writer.Using a few examples, let us see the kind of impact negative Gamma has on an option holder’s position.
| Option Type | Strike Price | Spot Price | Delta | Gamma |
| Call (Short) | ₹100 | ₹100 | -0.500 | -0.055 |
| ₹101 | -0.555 | -0.052 | ||
| ₹102 | -0.607 | -0.048 | ||
| ₹103 | -0.655 | -0.042 | ||
| ₹104 | -0.697 | -0.036 |
| Option Type | Strike Price | Spot Price | Delta | Gamma |
| Call (Short) | ₹100 | ₹100 | -0.500 | -0.055 |
| ₹99 | -0.445 | -0.052 | ||
| ₹98 | -0.393 | -0.048 | ||
| ₹97 | -0.345 | -0.042 | ||
| ₹96 | -0.303 | -0.036 |
Notice from the above tables that when the underlying price rose from ₹100 to ₹104, the Delta decreased in value and started moving towards -1. Given that a call writer is bearish on the underlying, a scenario wherein the underlying price is rising would cause the rate of the call writer’s losses to accelerate because of the impact of negative Gamma and Delta. On the other hand, when the underlying price fell from ₹100 to ₹96, the Delta increased in value and started moving towards 0. Such a situation would benefit the call writer.
| Option Type | Strike Price | Spot Price | Delta | Gamma |
| Put (Short) | ₹100 | ₹100 | 0.500 | -0.055 |
| ₹99 | 0.555 | -0.052 | ||
| ₹98 | 0.607 | -0.048 | ||
| ₹97 | 0.655 | -0.042 | ||
| ₹96 | 0.697 | -0.036 |
| Option Type | Strike Price | Spot Price | Delta | Gamma |
| Put (Short) | ₹100 | ₹100 | 0.500 | -0.055 |
| ₹101 | 0.445 | -0.052 | ||
| ₹102 | 0.393 | -0.048 | ||
| ₹103 | 0.345 | -0.042 | ||
| ₹104 | 0.303 | -0.036 |
Notice from the above tables that when the underlying price fell from ₹100 to ₹96, the Delta increased in value and started moving towards 1. Given that a put writer is bullish on the underlying, a scenario wherein the underlying price is falling would cause the rate of the put writer’s losses to accelerate because of the impact of positive Delta and negative Gamma. On the other hand, when the underlying price rose from ₹100 to ₹104, the Delta decreased in value and started moving towards 0. Such a situation would benefit the put writer.
Let us conclude this section by summarizing how positive and negative Gamma impacts the Delta of an option:
| Particulars | Delta (Δ) | Gamma (Γ) | Result |
| Long Call | Positive | Positive | The larger the rise in the underlying, the better it is for the call holder, as the +Γ would cause the +Δ to move closer and closer towards 1, making the trade more profitable |
| Short Call | Negative | Negative | If the underlying does not rise, the call writer would benefit, as the -Γ would cause the -Δ to move closer towards 0, which would enable the call writer to keep the option premium |
| Long Put | Negative | Positive | The larger the decline in the underlying, the better it is for the put holder, as the +Γ would cause the -Δ to move closer towards -1, making the trade more and more profitable |
| Short Put | Positive | Negative | If the underlying does not fall, the put writer would benefit, as the -Γ would cause the +Δ to move closer towards 0, which would enable the put writer to keep the option premium |
Put it in simple words, if you are long an option, you would want the absolute value of the Delta to move towards 1 and would thereby prefer a high value of Gamma. On the other hand, if you are short an option, you would want the Delta to move closer towards 0 and would thereby prefer a low value of Gamma.
Impact of Time to Expiration on Gamma
Earlier in this chapter, we saw how the moneyness of an option affects Gamma. We saw that Gamma tends to be at its peak when an option is ATM or NTM, and it tends to taper off as the option moves away from being ATM. We saw that Gamma reaches 0 when the option moves deep ITM or deep OTM. Now that we understand how option moneyness impacts Gamma, it is time to move on and understand how the time left to expiration affects Gamma.
In the previous chapter, we presented a table that highlighted how time to expiration affects Delta. Let us again present this table.
| Option Moneyness | Time to Expiration is… | Delta Values are… |
| ITM | Less | Higher |
| More | Lower | |
| OTM | Less | Lower |
| More | Higher | |
| ATM | Less | Lower |
| More | Higher |
In our discussion below, keep in mind that when we refer to shorter-dated options, we are referring to options that have less time to expiration. Similarly, when we refer to longer-dated options, we are referring to options that have more time to expiration. So, while the maturities (i.e. the time remaining to expiration) will differ, other characteristics such as underlying asset, underlying price, strike price etc. will remain the same.
Impact of Time to expiration on ITM Options
Let us start with options that are already ITM. By now, we understand that the absolute Delta of shorter-dated ITM options would be higher than the absolute Delta of longer-dated ITM options (which makes sense given that the probability of an ITM option expiring ITM gets higher and higher as the time passes by and expiration nears). From this it follows that, the Gamma of shorter-dated ITM options would be higher than that of longer-dated ITM options. However, remember that as the option moves deeper and deeper ITM, the absolute Delta will move closer and closer towards 1. This will eventually cause the Gamma of shorter-dated deep ITM options to fall below the Gamma of the longer-dated deep ITM options.
Impact of Time to expiration on OTM Options
Let us now talk about options that are already OTM. We know that the absolute Delta of shorter-dated OTM options would be lower than the absolute Delta of longer-dated OTM options (which makes sense given that the probability of an OTM option expiring ITM gets lower and lower as the time passes by and expiration nears). As the option moves from being ATM to OTM, the Gamma of shorter-dated OTM options would be higher than that of longer-dated OTM options. However, as the option moves deeper and deeper OTM, the absolute Delta will move closer and closer towards 0. This will eventually cause the Gamma of shorter-dated deep OTM options to fall below the Gamma of the longer-dated deep OTM options.
Impact of Time to expiration on ATM Options
Options that are ATM or NTM pose the greatest level of uncertainty in terms of whether they will be ITM at expiration. Because of this, as already stated earlier in this chapter, the Gamma of options that are ATM or NTM tend to be at the maximum. While Gamma of ITM or OTM options reduces as the time to expiration nears, that of ATM options increases as the time to expiration nears. As a result, when there is less time left to expiration, the Delta can change significantly for a 1-point change in the value of the underlying. Hence, shorter-dated ATM options tend to have much higher Gamma than longer-dated ATM options. And as the time passes by, the Gamma of ATM options only get larger and larger.
If the above concepts sounded a little heavy to digest, look at the table below. Compare the Gamma values in the table with the text above to better understand the impact of time on Gamma. Here, we have assumed the underlying price of ₹100 and the option type as Call option.
| Time to Expiration | Deep ITM | ITM | ATM | OTM | Deep OTM |
| Strike = 85 | Strike = 95 | Strike = 100 | Strike = 105 | Strike = 115 | |
| 1day | 0.000 | 0.000 | 0.305 | 0.000 | 0.000 |
| 15 days | 0.000 | 0.044 | 0.079 | 0.053 | 0.002 |
| 1 month | 0.003 | 0.040 | 0.055 | 0.047 | 0.010 |
| 3 months | 0.011 | 0.027 | 0.032 | 0.031 | 0.020 |
| 6 months | 0.012 | 0.020 | 0.022 | 0.023 | 0.019 |
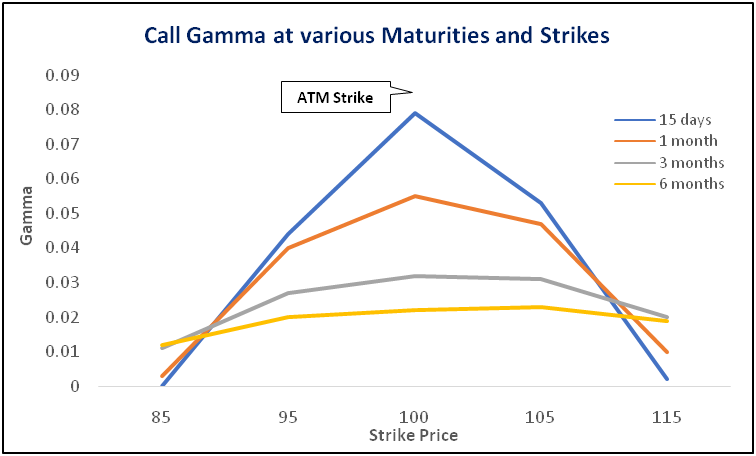
Notice from the table above that Gamma is very high for ATM options that are very close to expiry. For instance, with just a day left to expiry, the Gamma of an ATM call having a strike of ₹100 is 0.305, meaning that a 1-point change in the underlying price would cause the Delta to move up or down by 0.305. Notice that for ATM calls, the shorter-dated options have a larger Gamma than the longer-dated options. On the other hand, observe that when options move from ATM to ITM or OTM, the Gamma starts reducing. However, in case of options that are deep ITM or deep OTM, observe that the shorter-dated options have a lower Gamma than the longer-dated Gamma. The chart below shows the details of the above table in a graphical format.
Key things to remember here are that shorter-dated options have very high Gamma for ATM strikes but very low Gamma for deep ITM or OTM strikes. On the other hand, longer-dated options have relatively low Gamma for ATM strikes but relatively high Gamma for deep ITM or OTM strikes.
Impact of Volatility on Gamma
Besides option moneyness and time left to expiration, Gamma is also impacted by volatility. Let us now focus on understanding how volatility impacts the Gamma of an option. In the previous chapter on Delta, we presented a table that highlighted how volatility affects Delta. Let us present this table again for easy reference.
| Option Moneyness | Volatility is… | Delta Values are… |
| ITM | Low | Higher |
| High | Lower | |
| OTM | Low | Lower |
| High | Higher |
In the previous chapter, we saw that ITM options having low levels of volatility will have high Delta values, and vice versa. Similarly, we also saw that OTM options having low levels of volatility will have low Delta values, and vice versa. This concept will become easy to understand if you think of Delta as the probability of an option expiring ITM. Let us now try to understand how Gamma is affected by volatility, using a simple example. The table below shows Gamma values of a call option at various strikes and volatility and with 30 days left till expiration.
| Volatility | Deep ITM | ITM | ATM | OTM | Deep OTM |
| Strike = 85 | Strike = 95 | Strike = 100 | Strike = 105 | Strike = 115 | |
| 25% | 0.003 | 0.040 | 0.055 | 0.047 | 0.010 |
| 35% | 0.009 | 0.033 | 0.040 | 0.037 | 0.017 |
| 45% | 0.012 | 0.027 | 0.031 | 0.030 | 0.019 |
| 55% | 0.013 | 0.023 | 0.025 | 0.025 | 0.019 |
Notice in the table above that Gamma tends to be quite high for ATM options with low volatility, and it starts reducing as the volatility increases. The reason why this is the case is because when the underlying exhibits low volatility, the Delta changes swiftly once the option moves from ATM to either ITM or OTM than if the underlying were to exhibit high volatility. For instance, if an option moves from ATM to ITM, the Delta rises very quickly when the volatility is low because the odds of the option expiring ITM start to accelerate. On the other hand, if the volatility is high, then a move from ATM to ITM causes the Delta to rise at a relatively slower rate because the high level of volatility can still cause the option to move OTM by expiration. Meanwhile, if an option moves from ATM to OTM when the volatility is low, the Delta fallsrather quickly because the odds of the option expiring ITM start fading quickly. On the other hand, if the volatility is high, then a move from ATM to OTM causes the Delta to fall at a relatively slower rate because the high level of volatility can still cause the option to move ITM by expiration.
Using the same logic, we can see in the table that as the volatility increases, the Gamma of an ITM and OTM option reduces. Meanwhile, when an option is deep ITM, it will have an absolute Delta that is either equal to 1 or close to 1. Similarly, when an option is deep OTM, it will have a Delta that is equal to 0 or close to 0. We have seen that when the Delta is close to such extremes, their Gammas tend to be negligible. High levels of volatility, however, does cause Gamma of such deep ITM/OTM options to increase a bit. Hence, when an option is deep ITM or OTM, an increase in volatility causes the Gamma of such options to move higher as well.
Notice from the chart above that ATM options tend to have the highest Gamma. Also notice that as the volatility increases, the Gamma curve tends to become flatter. Observe that the Gamma curve tends to be very sensitive to price changes when volatility is low than it is to price changes when volatility is high.
Important concepts to remember about Delta
Let us now summarize some of the key learnings from this chapter:
-
Gamma is the rate of change in Delta for every 1 point move in the price of the underlying. So, while Delta measures the directional risk of an option, Gamma measures the changes in that directional risk.
-
Rising Gamma values mean that any change in the underlying price would lead to a greater change in the value of Delta, which in turn would lead to a greater change in the Option price, and vice versa.
-
Gamma is high when the option is NTM i.e., when the strike price and the underlying price are very close to each other. When the two start moving away from each other, Gamma starts reducing. When the option is deep ITM or deep OTM, the Gamma of that option is close to zero.
-
When a person buys an option, the Gamma is positive, and the buyer is said to be long the Gamma. Positive Gamma causes the Delta of a long option position to move towards 1 when the underlying price rises (in case of a call) or towards -1 when it drops (in case of a put). Similarly,positive Gamma causes the Delta of a long option position to move towards 0 when the underlying price falls (in case of a call) or rises (in case of a put).
-
When a person sells an option, the Gamma is negative, and the seller is said to be short the Gamma.When a person is short the Gamma, he would want the underlying to remain more or less stable. Sharp adverse movements against the direction of the short position would aggravate the losses of the writer.
-
The Gamma of shorter-dated ITM options would be higher than that of longer-dated ITM options. However, remember that as the option moves deeper and deeper ITM, the absolute Delta will move closer and closer towards 1. This will eventually cause the Gamma of shorter-dated deep ITM options to fall below the Gamma of the longer-dated deep ITM options.
-
As the option moves from being ATM to OTM, the Gamma of shorter-dated OTM options would be higher than that of longer-dated OTM options. However, as the option moves deeper and deeper OTM, the absolute Delta will move closer and closer towards 0. This will eventually cause the Gamma of shorter-dated deep OTM options to fall below the Gamma of the longer-dated deep OTM options.
-
The Gamma of ATM options increase as the time to expiration nears. As a result, when there is less time left to expiration, the Delta can change significantly for a 1-point change in the value of the underlying. Hence, shorter-dated ATM options tend to have much higher Gamma than longer-dated ATM options.
-
Gamma tends to be quite high for ATM options with low volatility, and it starts reducing as the volatility increases.
-
As the volatility increases, the Gamma of an ITM and OTM option reduces.
-
When an option is deep ITM or OTM, an increase in volatility causes the Gamma of such options to move higher as well.
Next Chapter
Comments & Discussions in
FYERS Community
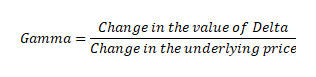


pavan commented on January 30th, 2020 at 12:33 AM
When i sell or buy one lot of Nifty, how to calculate the taxes ? I mean how to calculate the IGST , Stamp duty, transaction charges, Ibt, Cm charges ?
Shriram commented on January 31st, 2020 at 10:07 PM
Hi Pavan, kindly use the brokerage calculator that is available on our website
Shriram commented on January 31st, 2020 at 10:06 PM
For this, kindly use the brokerage calculator that is available on our website
Aniket commented on April 25th, 2020 at 12:02 AM
Sir, I have confusion on the Delta Gamma table of various longs and short position of call and put option given in table.
Its given in table that Delta of short put option has to be positive and gama has to be negative
However, In Previous delta topic it has been written that "Delta of put option is always negative"
Theta has to be positive for option sellers
So please help me resolve this confusion as in option calculator of fyersone software almost maximum put option having negative Delta. kindly help me with this
Shriram commented on April 25th, 2020 at 7:45 AM
Hi Aniket, whenever anyone speaks of options in general, it is by default spoken from the buyer's standpoint. For instance, think about a Call option. When we speak generally, we say a Call option is bullish, which is in fact true. However, when looked at from a seller's perspective, things change. For instance, a Call seller is bearish because he /she has written a Call option; while a Put seller is bullish because he/she has written a Put option. In options parlance, one party's gain is another party's loss. Same logic applies to Greeks as well. If one Greek for a long option position is positive, the corresponding Greek for the corresponding short option position will be negative, and vice versa.
Coming to your first question, in the Chapter on Delta, when we said Delta of a Put is always negative, it is a general statement. However, things change when looked at from a seller's standpoint for the reasons mentioned above.
Coming to your second question, most of the option calculators assign signs to Greeks from a general standpoint. Hence, in an option calculator, you will see +Delta, +Gamma, +Vega, -Theta, and +Rho for a Call option; and -Delta, +Gamma, +Vega, -Theta, and -Rho for a Put option.
I hope that helps address your query.
Aniket commented on April 25th, 2020 at 9:12 AM
Sir, My question is what should be option geek for option sellers
lets say PUT
as per study material
Delta- negative
gama- positive
theta- positive
vega- negative
Now i need to find a strike price which has all these greek condition satisfied
But in reality in option calculator suppose i take nifty for expiry 30 April
I find maximum put options deltas negative instead of positive
now what to do in this case?, from where do I bring positive delta matching with other option greeks for shorting put options?
aniket commented on April 25th, 2020 at 9:16 AM
Correction in above comment
For Put seller
Delta - positive
Gama- negative
theta- positive
vega- negative
I am unable to find positive delta with all other geeks condition matching for put options.. I find negative delta for most put options... kindly help me
Shriram commented on May 3rd, 2020 at 7:27 PM
Hi Aniket, as i said in my previous comment, by default option calculators are designed from a buyer's point of view.
So in case of a Call option, the calculator would show you the following signs: + Delta, +Gamma, +Vega, and -Theta.
Similarly, in case of a Put option, the calculator would show you the following signs: -Delta, +Gamma, +Vega, and -Theta.
It doesn't matter whether you are an option buyer or a seller, the signs would appear as are mentioned above in an option calculator.
That said, when selling an option, think logically. Remember that what ever is a buyer's gain is a seller's loss, and vice versa. Let us take the example of a Put option. For a Put buyer, rising volatility benefits the position; while for a Put seller, rising volatility hurts the position. Similarly, for a Put buyer, time decay is an enemy; while for a Put seller, time decay is a friend. Similarly, a Put buyer would want the absolute Delta to increase as this would make the option premium more sensitive to changes in underlying price; while a Put seller would want the absolute Delta to decrease as this would make the option premium less sensitive to changes in underlying price.
Again remember, if a particular Greek is positive for long position, then that Greek will be negative for the corresponding short position.
James Raj commented on May 14th, 2020 at 8:49 AM
Can someone please explain how Delta is arrived in the third line of exsmples , for example Call 100 spot price 103 u show option price 7.3 , Delta 0.56 gamsa 1 ( how u get . 56 Delta??)
Shriram commented on May 14th, 2020 at 8:28 PM
Hi James, the Greeks are calculated by an option calculator using the six inputs - underlying price, strike price, time to expiration, volatility, dividend (if applicable), and interest rates. Once you input each of these figures into the option calculator, it will calculate each of the Greeks using the theoretical Option Pricing model (usually the Black Scholes Merton model). The 0.56 Delta value that you are talking about is arrived in such a way. In the real world, most Greeks keep changing every moment as and when any of the aforementioned metrics change.