School of Stocks

In this chapter, we will talk in detail about the Delta of an option. We shall first explain what the Delta of an option means, before proceeding to the practical application of this vital option Greek. Having a strong understanding of option Delta is very critical because it helps a person understand how the change in the price of the underlying will influence the price of the option in terms of both direction and magnitude. Depending upon the value of the Delta, a person can also assess the risk that is involved in an option trade.

Delta defined

Delta is the rate of change in the price of an option for every 1 point move in the price of the underlying asset. In other words, delta measures the directional risk of an option. The underlying asset in question could be equity, index, currency, commodity, bond, interest rate etc. Put it in the form of an equation, delta can be calculated as:

As we know by now, the value of a call option moves higher while that of a put option moves lower when the price of the underlying rises. Similarly, the value of a call option moves lower while that of a put option moves higher when the price of the underlying falls. In other words, the value of a call option and the underlying price are directly proportional; while the value of a put option and the underlying price are inversely proportional. Because of this correlation with the underlying price, a call option will have positive delta; while a put option will have negative delta. The delta of a call option will fluctuate within a range of 0 and 1; while that of a put option will fluctuate within a range of 0 and -1. Let us highlight this again.

Delta of a call option will move between 0 and 1

Delta of a put option will move between 0 and -1

The question that may arise in your mind is what exactly does this mean? Well, let us explain this using a simple example.

Let us first consider the case of a call option. Let us assume that the current price of the underlying is ₹100. Let us also consider that a call option on this underlying is priced at ₹5 and has a delta of 0.50. A few days down the line, let’s say that the price of the underlying has risen to ₹108. Given that the price of the underlying has risen by ₹8, assuming all else constant, the value of the call option will go up by ₹4 (₹8 * 0.50). That is, the price of the call option will now be worth ₹9 (₹5 + ₹4). On the other hand, what if a few days down the line, the price of the underlying dropped to ₹94? In this case, given that the price of the underlying has fallen by ₹6, the value of the call option will go down by ₹3 (-₹6 * 0.50). That is, the price of the call option will now be worth ₹2 (₹5 - ₹3).

Let us now consider the case of a put option. Let us assume that the current price of the underlying is ₹100. Let us also consider that a put option on this underlying is priced at ₹6 and has a delta of -0.50. A few days down the line, let’s say that the price of the underlying has dropped to ₹90. Given that the price of the underlying has dropped by ₹10, the value of the put option will go up by ₹5 (-₹10 * -0.50). That is, the price of the put option will now be worth ₹11 (₹6 + ₹5). On the other hand, what if a few days down the line, the price of the underlying rose to ₹104? In this case, given that the price of the underlying has risen by ₹4, the value of the put option will go down by ₹2 (₹4 * -0.50). That is, the price of the put option will now be worth ₹4 (₹6 - ₹2).

To make things simpler, let us now present a few examples in a tabular format.

Option Type	Delta	Option Price	New option price for a ₹1 rise in the underlying	New option price for a ₹1 fall in the underlying
Call	0.80	₹10	₹10.80	₹9.20
Call	0.50	₹7	₹7.50	₹6.50
Call	0.20	₹3	₹3.20	₹2.80
Put	-0.20	₹4	₹3.80	₹4.20
Put	-0.50	₹6	₹5.50	₹6.50
Put	-0.80	₹9	₹8.20	₹9.80

Notice that as the underlying price goes up by ₹1, the value of a call option increases by the amount of delta, while that of a put option decreases by the amount of delta. On the other hand, as the underlying price goes down by ₹1, the value of a put option increases by the amount of delta, while that of a call option decreases by the amount of delta. Plain simple mathematics here. In fact, assuming everything else is constant, we can set a formula to calculate the new option price as shown below:

New Option price = Old Option price + Delta * (New underlying price - Old underlying price)

So, if the new underlying price is ₹105, old underlying price is ₹100, old call option price is ₹10, and call delta is 0.6, the new option price would be ₹13 [₹10 + 0.6 * (₹105 - ₹100)]. On the other hand, if the new underlying price is ₹105, old underlying price is ₹100, old put option price is ₹10, and put delta is -0.6, the new option price would be ₹7 [₹10 + (-0.6) * (₹105 - ₹100)].

Similarly, if the new underlying price is ₹92, old underlying price is ₹100, old call option price is ₹10, and call delta is 0.5, the new option price would be ₹6 [₹10 + 0.5 * (₹92 - ₹100)]. On the other hand, if the new underlying price is ₹92, old underlying price is ₹100, old put option price is ₹10, and put delta is -0.5, the new option price would be ₹14 [₹10 + (-0.5) * (₹92 - ₹100)].

In the above equation, keep in mind the sign of delta (positive for call option and negative for put option).

Now that we have understood how to calculate the new option price for a given change in the underlying price and at a given delta, it is time to move on and dig in deeper towards understanding the concept of delta.

Another way of looking at Delta

So far, we have defined delta as the rate of change in the price of an option for every 1 point move in the price of the underlying asset. There is another way of looking at delta. That is, delta is the probability of the option expiring In-the-Money (ITM). For instance, a delta of 0.5 means there is a 50% probability of a call option expiring ITM, a delta of 0.8 means there is an 80% probability of a call option expiring ITM, and so forth. Similarly, a delta of -0.6 means there is a 60% probability of a put option expiring ITM, a delta of -0.1 means there is a 10% probability of a put option expiring ITM, and so forth. Keep in mind that a call option will have positive delta, while a put option will have negative delta.

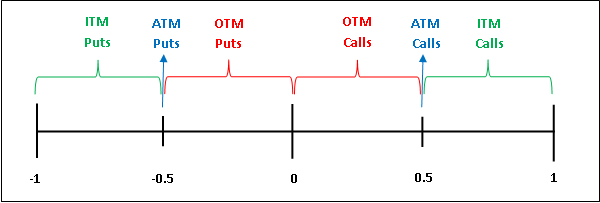
Impact of Option Moneyness on Delta

We now come to an important part of this chapter, which is understanding how option moneyness impacts the value of the option delta. As we have seen in the previous chapters, an option could be in any one of the three states: In-the-Money (ITM), At-the-Money (ATM), or Out-of-the-Money (OTM). Just recapping, a call option is ITM if the strike price of the call is less than the spot price, ATM if the strike price of the call is equal to the spot price, and OTM if the strike price of the call is greater than the spot price. Similarly, a put option is ITM if the strike price of the put is greater than the spot price, ATM if the strike price of the put is equal to the spot price, and OTM if the strike price of the put is less than the spot price.

The state of the option moneyness has an impact on the value of both call delta and put delta. A call option that is ITM will have a delta that is greater than 0.5, a call option that is ATM or almost ATM will have a delta that is equal to or very close to 0.5, while a call option that is OTM will have a delta that is less than 0.5. Similarly, a put option that is ITM will have a delta that is less than -0.5, a put option that is ATM or almost ATM will have a delta that is equal to or very close to -0.5, while a put option that is OTM will have a delta greater than -0.5.Let us put this in a tabular and graphical format for ease of remembering:

Option Type	Option Moneyness	Delta
Call	ITM	>0.5 and ≤1.0
	ATM	0.5
	OTM	≥0.0 and <0.5
Put	ITM	<-0.5 and ≥-1.0
	ATM	-0.5
	OTM	≤0.0 and >-0.5

The deeper the option is ITM, the closer the delta would be either towards 1 (in case of a call option) or towards -1 (in case of a put option). Meanwhile, the deeper the option is OTM, the closer the delta would be towards 0 for both the options. Knowing where the delta of a call and a put option is can play a key role in the success of an option trade.

Knowing the position of Delta is critical

As stated above, knowing where the delta of a call and a put option is can play a key role in the success of an option trade. Let us now understand why this is the case. Earlier, we had defined delta as the rate of change in the price of an option for a given change in the price of the underlying. The higher the absolute value of the delta, the greater would be the move in the option price for a given move in the underlying price, and vice versa. In other words, the higher the absolute value of delta, the higher would be the risk/reward potential of an option trade.

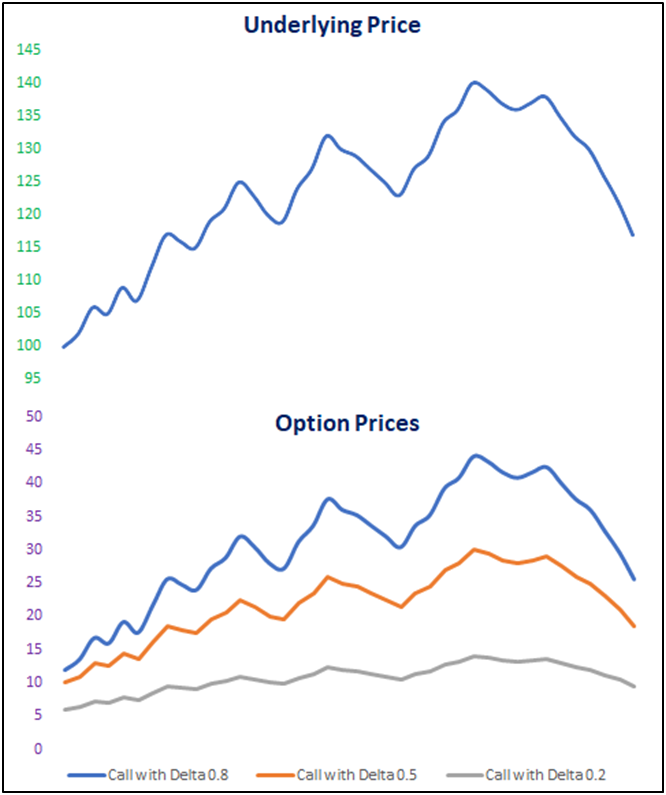
Before proceeding further, keep in mind that the delta of the underlying is 1. This is because if you buy, say, 100 stocks and if the price of that stock goes up by, say, ₹1, you profit ₹100. That is, for every 1 point move in the value of the underlying, the profit/loss potential is 100% of that 1 point move.Options, on the other hand, have varying delta depending on whether those options are ITM, ATM, or OTM. As a rule, options that have higher delta are more responsive to changes in the price of the underlying than are options that have lower delta. For instance, consider two Call options with the same underlying and the same expiration date but with different strike prices: One option has a strike price of ₹100 and a delta of 0.7, while the other option has a strike price of ₹110 and a delta of 0.3. If the price of the underlying rises by ₹8, the option that has a delta of 0.7 will rise by ₹5.6 (₹8*0.7), while the option that has a delta of 0.3 will rise by only ₹2.4 (₹8*0.3). As we can see, the reward potential is higher for options with higher delta than options with lower delta. That said, the risk potential is also higher for options with higher delta than options with lower delta. For instance, considering the same example as above, if the price of the underlying instead falls by ₹8, the option that has a delta of 0.7 will fall by ₹5.6, while the option that has a delta of 0.3 will fall by only ₹2.4. Let us now illustrate this graphically.

The above chart shows the movement in the price of Call options for a corresponding move in the price of the underlying. The three Call options above have a delta of 0.8, 0.5, and 0.2. Observe closely the movement in the price of the options. Notice that the Call option that has a delta of 0.8 (blue line) is much more responsive to changes in the price of the underlying. On the other hand, notice that the Call option that has a delta of 0.2 (grey line) is least responsive to changes in the price of the underlying. Neither did this option rise much during the up move in the price of the underlying, nor did it fall much during the down move in the price of the underlying.

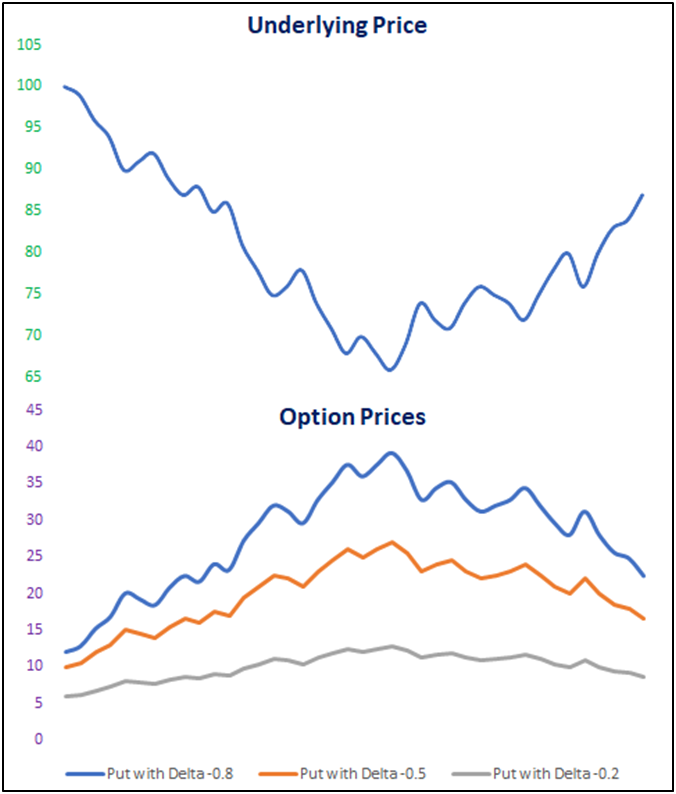
Meanwhile, the above chart shows the movement in the price of Put options for a corresponding move in the price of the underlying. The three Put options above have a delta of -0.8, -0.5, and -0.2. Notice that the Put option that has a delta of -0.8 (blue line) is much more responsive to changes in the price of the underlying. On the other hand, notice that the Put option that has a delta of -0.2 (grey line) is least responsive to changes in the price of the underlying.

Why is this important?

The reason why looking at Delta is important is because, depending on its value, Delta influences the price of an option. Keep in mind that options have a finite date. In Chapter 3, we saw that as time passes by, the time value component of the option price will decay. During the initial life of an option contract, the pace of time decay will be slow. However, as the time to expiration reduces, the pace of time decay will start accelerating. During the latter stages of an option contract, the pace of time decay will be very fast. Given this, the odds are stacked against the buyer in making a profitable trade. Remember, if the underlying price does not move much, the buyer of an option can lose money because the time value component of the option price will erode.

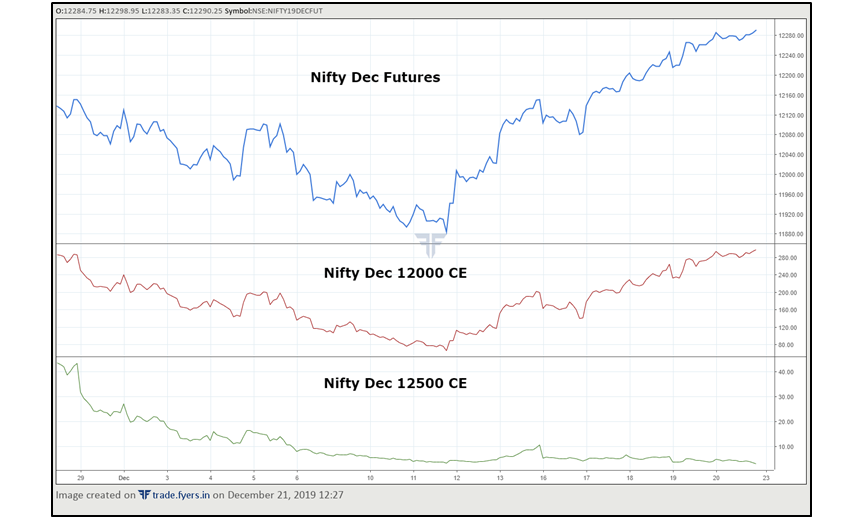
Options that are ITM will be more expensive than options that are ATM, which in turn will be more expensive than options that are OTM. We have also seen that options that are ITM will have higher delta (in absolute value terms) than options that are ATM, which in turn will have a higher delta than options that are OTM. Often, people who are new to options trading are tempted to buy options that are deepOTM, just because they are very cheap. While there is nothing wrong in doing this, one must keep in mind that the odds of deep OTM options gaining in value are low, because of the time value component and because they have a lower delta. This was evident in the two charts that we posted above. Notice that the OTM options did not change much despite the noticeable change in the price of the underlying asset.

Notice in the chart above that while Nifty rallied from around 11900 to around 12300 (a price gain of over 3%), the option price of 12000 CE (which became ITM when Nifty crossed 12000) rose from around ₹70 to around ₹300 (a price gain of around 300%); while the option price of 12500 CE (which is OTM) has been essentially unchanged. So, if someone had bought this OTM call option, he would not have made money on the trade, despite going right on the direction of the underlying (remember, buying a call option means one is bullish on the underlying). On the other hand, had he instead bought an option that was either ITM or ATM (12000 CE in the above case), he would have made strong gains considering the higher delta of such options.

Hence, it is not just about selecting the right type of option, but also about the right strike price and the right delta levels when entering an option trade. Buying an OTM option just because it is cheap and without taking into consideration other parameters is a recipe for losing capital. One should buy an OTM option only when there is greater time left to expiration and when one has a view that the underlying with rise swiftly (in case of a call option) or fall swiftly (in case of a put option) for the price of that option to gain in value. Always keep in mind that OTM options are cheap for a reason. They have a delta whose absolute value is less than 0.5, meaning they have less than 50% chance of expiring ITM. The deeper the option is OTM, the lower will be its delta, meaning the lower will be the probability of that option moving ITM by the expiration date.

Impact of Time on Delta

So far, we have mostly talked about the impact of underlying price and option moneyness on option delta. Now, let us talk about another key factor that impacts delta: the time left to expiration. Let us highlight the relationship between delta and time to expiration. For ITM options, the deltas of options that are closer to expiry are higher than the deltas of options that are farther from expiry. Why? Because, there are greater odds of ITM options expiring ITM when there is little time left to expiration than when there is more time left to expiration. On the other hand, for options that are OTM, the effect is opposite i.e. the deltas of options that are closer to expiry are lower than the deltas of options that are farther from expiry. Why? Because, there are lower chances of OTM options expiring ITM when there is little time left to expiration than when there is more time left to expiration. Let us now explain this concept using four examples. For each of the four examples, keep in mind that at the time of writing, Nifty was quoting around 11200.

ITM Call option example:What are the odds of an ITM Nifty call option having a strike price of, say, 10000 expiring ITM by, say, the end of next week? I would say 99%. However, what are the odds of this same ITM call option expiring ITM by, say, the end of CY20? Now, I would say 78%. Notice the difference? As there is less time left to expiration, the odds that an ITM call option will expire ITM will be higher. However, as the time left to expiration is high, the probability that an ITM call option will expire ITM reduces and, on a relative basis, tends to move closer towards 0.5.

OTM Call option example: What are the odds of an OTM Nifty call option having a strike price of, say, 15000 expiring ITM by, say, the end of next week? I would say 2%. However, what are the odds of this same OTM call option expiring ITM by, say, the end of CY20? Now, I would say 30%. Notice the difference? As there is less time left to expiration, the odds that an OTM call option will expire ITM will be lower. However, as the time left to expiration is high, the probability that an OTM call option will expire ITM increases and, on a relative basis, tends to move closer towards 0.5.

ITM Put option example: What are the odds of an ITM Nifty put option having a strike price of, say, 15000 expiring ITM by, say, the end of next week? I would say 99%. However, what are the odds of this same ITM put option expiring ITM by, say, the end of CY20? Now, I would say 76%. Notice the difference? As there is less time left to expiration, the odds that an ITM put option will expire ITM will be higher. However, as the time left to expiration is high, the probability that an ITM put option will expire ITM reduces and, on a relative basis, tends to move closer towards -0.5.

OTM Put option example: What are the odds of an OTM Nifty Put option having a strike price of, say, 10000 expiring ITM by, say, the end of next week? I would say 1%. However, what are the odds of this same OTM put option expiring ITM by, say, the end of CY20? Now, I would say 29%. Notice the difference? As there is less time left to expiration, the odds that an OTM put option will expire ITM will be lower. However, as the time left to expiration is high, the probability that an OTM put option will expire ITM increases and, on a relative basis, tends to move closer towards -0.5.

Let us now present this all in a tabular format for easy reference. Kindly note that whether the option is a call or a put doesn’t matter:

Option Moneyness	Time to Expiration is…	Delta Values are…
ITM	Less	Higher
ITM	More	Lower
OTM	Less	Lower
OTM	More	Higher
ATM	Less	Lower
ATM	More	Higher

We will talk more about how time impacts option price in Chapter 8, wherein we will cover Theta.

Impact of Volatility on Delta

We will now briefly talk about the impact of volatility on Delta. For ITM options, the Delta will be higher if the underlying has low volatility and lower if the underlying has high volatility. This is because the probability of an ITM option expiring ITM is higher when volatility is low (low volatility means less likelihood of a big move in the price of the underlying). However, when volatility is high, the probability that an ITM option would expireITM reduces (high volatility means greater likelihood of a big move in the price of the underlying), causing the delta to reduce.Similarly, for OTM options, the delta will be lower if the underlying has low volatility and higher if the underlying has high volatility. Again, this is because the probability of an OTM option expiring ITM is lower when volatility is low. However, when volatility is high, the probability that an OTM option would expire ITM increases, causing the delta to increase too.

Let us now present this all in a tabular format for easy reference. Kindly note that whether the option is a call or a put doesn’t matter:

Option Moneyness	Volatility is…	Delta Values are…
ITM	Low	Higher
ITM	High	Lower
OTM	Low	Lower
OTM	High	Higher

We will talk more about how volatility impacts option price in Chapter 7, wherein we will cover Vega.

Delta is Dynamic

The value of Delta is not stable but is rather dynamic. In other words, the value of delta keeps changing with changes in other variables that are inputted in the option pricing model. These include the spot price, volatility, time to expiration, interest rates, and dividend (if any). If the values of any of these variables change, so will the value of delta. It is important to understand changes in delta, because this change in delta will have an impact on the success of the option trade. Remember that an ITM option will have a delta whose absolute value is greater than 0.5, an ATM option will have a delta whose absolute value is 0.5, and an OTM option will have a delta whose absolute value is less than 0.5.

As the underlying price changes, the option can move from OTM to ATM and then ITM. Similarly, an option can also move from ITM to ATM and then OTM. As this change happens, the value of delta will also change. For instance, when an option is OTM, its delta will be less than 0.5. But, if the underlying price changes, because of which this option moves ITM, its delta will now be more than 0.5. Given that the option is now ITM, it will be more responsive to changes in the underlying price. It is very important to be aware of such changes. As the option moves further ITM, the delta will keep increasing, causing the option price to be more and more sensitive to changes in the underlying price; and as the option moves further OTM, the delta will keep decreasing, causing the option price to be less and less sensitive to changes in the underlying price.

Let us now take a hypothetical example. Let us assume that a Call option is ITM,has a delta of 0.65, and an option price of ₹15. Let us say that in a few days, the price of the underlying declined by ₹10, causing this option to move OTM. Let us assume that the delta has now declined to 0.40 and the option price has dropped to ₹8. Let us now assume that in a few days, the price of the underlying rose by ₹10, thereby rising back to its old price. However, given the lower delta and the impact of time decay, the option price has risen to just, say, ₹11. Notice the difference? While the underlying price fell and has now recovered back to its old price, the option price on the other hand has not recovered to its old price. One reason for this is the change in delta, which has made the option less sensitive to change in the underlying price. Hence, whenever one needs to create new positions in options, or more importantly, has already created one, it is very important to pay a close attention to what the option’s delta is doing.

In the next chapter, we will talk about how to measure the rate of change in delta, so that one can get an idea of how to calculate the new delta whenever the price of the underlying changes. In a later chapter, we will again talk about delta, to understand another important concept called “Delta Hedging”.

Important concepts to remember about Delta

Let us now summarize some of the key learnings from this chapter:

Delta measures the rate of change in the price of an option for every 1 point move in the price of the underlying asset
The delta of a call option will fluctuate within a range of 0 and 1
The delta of a put option will fluctuate within a range of 0 and -1
For a change in the price of the underlying, the new option price can be calculated as Old Option price + Delta * (New underlying price - Old underlying price), with an assumption that everything else remains constant
Delta can also be looked at as the probability of the option expiring ITM. For instance, a delta of 0.3 means there is a 30% change of an option expiring ITM
ITM call options will have delta between 0.5 and 1
ATM call options will have delta of 0.5
OTM call options will have delta between 0 and 0.5
ITM put options will have delta between -0.5 and -1
ATM put options will have delta of -0.5
OTM put options will have delta between 0 and -0.5
Delta of the underlying is 1
Options that have higher delta are more responsive to changes in the price of the underlying than are options that have lower delta
For ITM options, the deltas of options that are closer to expiry are higher than the deltas of options that are farther from expiry
For OTM options, the deltas of options that are closer to expiry are lower than the deltas of options that are farther from expiry
For ATM options, the deltas of options that are closer to expiry are lower than the deltas of options that are farther from expiry
For ITM options, the delta will be higher if the underlying has low volatility and lower if the underlying has high volatility
For OTM options, the delta will be lower if the underlying has low volatility and higher if the underlying has high volatility
The value of delta keeps changing with changes in other variables that are inputted in the option pricing model
As the underlying price changes, the option can move from OTM to ATM and then ITM. Similarly, an option can also move from ITM to ATM and then OTM
As the option moves further ITM, the delta will keep increasing, causing the option price to be more and more sensitive to changes in the underlying price
As the option moves further OTM, the delta will keep decreasing, causing the option price to be less and less sensitive to changes in the underlying price

Next Chapter

Gamma

8 Lessons

In this chapter, we will study about a derivative of Delta, called Gamma. We will start the chapter by introducing Gamma, including how it impacts the Delta of an option. We will then talk about how Gamma is impacted by option moneyness, time to expiration, and volatility.

Vega - Part 1

4 Lessons

In this chapter, we shall introduce the concept of Volatility. We shall talk about how volatility is calculated and the two most commonly used types of volatility in options parlance: Historical Volatility and Implied Volatility. The chapter acts as a precursor to our main topic of discussion on Vega, which will be covered in the next chapter.

Comments & Discussions in

FYERS Community

Responses

Mihir commented on January 7th, 2020 at 8:24 PM
Hello Sir,
Greetings...
I would like to know whether you conduct any weekend classes on basics to advanced study on Share market.

Shriram commented on January 23rd, 2020 at 9:59 PM
Not at present Mihir. But we plan to do webinars on the same in the coming months. So stay tuned!

Rahul Gupta commented on January 25th, 2020 at 4:27 PM
Want to learn Option
I have zero knowledge in option

Shriram commented on January 25th, 2020 at 5:00 PM
Hi Rahul, we are covering Options in detail in our module, starting right from the basics all the way to advanced content. If you are new to Options, I would highly recommend you to go through each of our chapters on Options. We would be adding more chapters on Options going forward.

rajiv commented on March 29th, 2020 at 2:17 AM
where can we find delta gamma of stock we are trading in website at least historical delta figure of any stock indices

Shriram commented on April 20th, 2020 at 7:42 AM
Hi Rajiv, you can find Option Greeks on the Fyers One platform. These are at present available on an EOD basis.

Mahesh commented on June 23rd, 2020 at 3:25 PM
Sir,
As you have explained in another module that IV(implied value) can be seen in the option chain. Where can i get the value of various options Greeks?

Abhishek Chinchalkar commented on June 26th, 2020 at 8:45 AM
Hi Mahesh, you can find Option Greeks on the Fyers One platform. These are at present available on an EOD basis.

1. Introduction to Stock Markets

2. Technical Analysis

3. Fundamental Analysis

4. Commodities

5. Currencies

6. Options

7. Options Strategies

8. Futures

9. Intermarket Analysis and Sector Rotation

10. Risk and Money Management

11. Trading Psychology

Delta