LONG CALL BUTTERFLY
| Strategy Details | |
| Strategy Type | Neutral, but bias can tilt slightly depending on the positioning of the middle strike at initiation |
| # of legs | 4 (Long 1 Lower Strike Call + Short 2 Middle Strike Calls + Long 1 Higher Strike Call) |
| Maximum Reward | Middle Strike Price - Lower Strike Price - Net Premium Paid |
| Maximum Risk | Limited to the extent of net premium paid |
| Lower Breakeven Price | Lower Strike Price + Net Premium Paid |
| Upper Breakeven Price | Higher Strike Price - Net Premium Paid |
| Payoff Calculation | Payoff of lower strike Long Call+ (2 * Payoff of middle strike Short Call) + Payoff of higher strike Long Call |
Explanation of the Strategy
A Long Call Butterfly is a strategy that involves buying one lower strike Call, selling two middle strike Callshaving the same strike, and buying one higher strike Call. The lower strike Call that is bought is an ITM Call, while the higher strike Call that is bought is an OTM Call. Meanwhile, the two middle strike Calls that are sold are usually ATM, but they can sometimes be slightly ITM or slightly OTM as well. All the four options that are transacted must belong to the same underlying and must have the same expiration date. An important thing to keep in mind is that the lower and the higher strike must be equidistant from the middle strike. In other words, the price difference between the lower strike and the middle strike must equal the price difference between the middle strike and the higher strike.
The net cost of this strategy is typically low because of the two middle strike Calls that are sold. Also, maximum loss under this strategy is limited no matter how higher or lower the underlying price moves. Because of these features, this strategy is quite popular among option traders. However, it must be kept in mind that this strategy benefits when the underlying is trading within a relatively narrow range and is exhibiting declining volatility. An expansion in volatility could be detrimental to the success of the trade.
This strategy has two breakeven points: lower and upper. The trader would be in a profitable position when the underlying price is in between the two breakeven points. On the flip side, the trader would incur losses when the underlying is trading either below the lower breakeven point or above the higher breakeven point. Meanwhile, maximum profit under this strategy is limited and occurs when the underlying price rises to the middle strike. On the flip side, maximum loss under this strategy is also limited and occurs when either the underlying price falls below the lower strike price or rises above the higher strike price.
Depending on the strike price chosen for selling the Calls, this strategy can be neutral, slightly bullish, or slightly bearish. Remember, maximum profit under this strategy occurs when the underlying price is exactly at the middle strike. As a result, this strategy is considered neutral if the two middle strike Calls that are sold are ATM Calls. In this case, the trader is of the view that the underlying price will stay range bound. Meanwhile, this strategy is considered slightly bullish if the two middle strike Calls that are sold are slightly OTM. In this case, the trader is of the view that the underlying price will rise slightly to move to the middle strike. Finally, this strategy is considered slightly bearish if the two middle strike Calls that are sold are slightly ITM. In this case, the trader is of the view that the underlying price will fall slightly to move to the middle strike.
Benefits of the Strategy
-
This strategy is a low cost strategy as the cost of the Calls bought is offset to a great extent by the two middle strike Calls sold
-
Maximum loss is limited no matter how higher or lower the price of the underlying goes
-
The risk to reward ratio under this strategy can be quite attractive
Drawbacks of the Strategy
-
An unexpected rise in volatility can hurt the profitability of the trade, especially when the underlying price is within the two breakeven points
-
Because this strategy involves selling two options, it will require a greater margin in your trading account at the time of initiation
-
A potential to lose the entire net debit amount, in case the underlying falls below the lower strike or rises above the higher strike
Strategy Suggestions
-
See that your view on the underlying is range bound
-
Avoid executing this strategy when you expect volatility to pick up. Instead this strategy works well when volatility is declining
-
Ensure that the distance between the lower strike and the middle strike is equal to that between the middle strike and the higher strike
-
The spread between the strikes will be a trade-off between the cost/risk of the strategy and the reward potential
-
The narrow the difference between the strikes, the smaller will be the cost/risk but so would be the reward, and vice versa
-
Because this is a range bound strategy that benefits from low volatility, ensure that you execute this strategy when the expiration is not far off, as giving too much time could cause the underlying price to move beyond one of the two breakeven points
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Long Call Butterfly
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to peak out above zero when the underlying price is near the lower strike and bottom out below zero when the underlying price is near the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is negative and is at its lowest point at initiation. As the underlying price moves away from the middle strike and approaches either the lower or the higher strike, Gamma tends to move into positive before peaking out around these extreme strikes. |
| Vega |
Vega is negative and is at its lowest point at initiation, meaning the negative impact of a rise in volatility is the highest at the middle strike. Volatility hurts as long as the position in profitable. That said, Vega turns positive when the position becomes unprofitable, meaning a rise in volatility now starts helping the position. |
| Theta |
Theta is positive and is at its highest point at initiation, meaning time decay is most helpful around the middle strike. Time decay benefits the position as long as it is profitable. That said, Theta turns negative when the position becomes unprofitable, meaning time decay now starts hurting the position. |
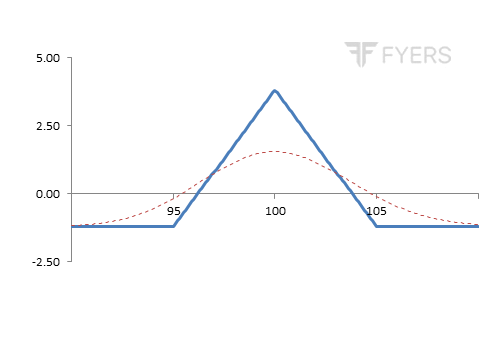
Payoff of Long Call Butterfly
The above is the payoff chart of a long Call Butterfly. Notice that the lower and the higher strike are equidistant from the middle strike. Observe that if the underlying price falls below the lower strike or rises above the higher strike, the trader suffers the highest loss for this strategy, which is limited to the extent of net premium paid. Also observe that the maximum profit for this strategy occurs when the underlying price is exactly at the middle strike. As the underlying price starts moving away from the middle strike, notice that the profitability starts reducing as well.
Example of Long Call Butterfly
Let us say that Mr. ABC has closely observed the chart of Nifty and is of the opinion that it will remain very range bound in the short-term. Based on this, let us say that he has decided to initiate a long Call Butterfly strategy, wherein he will buy 1 ITM 9700 Call at ₹390, sell 2 ATM 9850 Calls at ₹300 each, and buy 1 OTM 10000 Call at ₹230. Let us summarize the details of the strategy below:
-
Strike price of ITM longCall = 9700
-
Strike price of ATM shortCalls = 9850
-
Strike price of OTM long Call = 10000
-
Quantity of Calls bought = 2 lots (at different strikes)
-
Quantity of Calls sold = 2 lots (at same strike)
-
LongCall premium (lower strike) = ₹390
-
Short Call premium (middle strike) = ₹300
-
LongCall premium (higher strike) = ₹230
-
Net Debit = ₹20 (390 + 230 - 2 * 300)
-
Net Debit (in value terms) = ₹1,500 (20 * 75)
-
Lower Breakeven point = 9720 (9700 + 20)
-
Upper Breakeven point = 9980 (10000 - 20)
-
Maximum reward = ₹9,750 ((9850 - 9700 - 20) * 75)
-
Maximum risk = ₹1,500
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 8000 | Loss of ₹1,500 | Payoff = [Maximum of (8000-9700,0)-390]+[2*{300-maximum of (8000-9850,0)}] + [Maximum of (8000-10000,0)-230]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-9700,0)-390]+[2*{300-maximum of (9000-9850,0)}] + [Maximum of (9000-10000,0)-230]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9700 | Loss of ₹1,500 | Payoff = [Maximum of (9700-9700,0)-390]+[2*{300-maximum of (9700-9850,0)}] + [Maximum of (9700-10000,0)-230]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9710 | Loss of ₹750 | Payoff = [Maximum of (9710-9700,0)-390]+[2*{300-maximum of (9710-9850,0)}] + [Maximum of (9710-10000,0)-230]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9720 | No profit, No loss | Payoff = [Maximum of (9720-9700,0)-390]+[2*{300-maximum of (9720-9850,0)}] + [Maximum of (9720-10000,0)-230]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 9800 | Profit of ₹6,000 | Payoff = [Maximum of (9800-9700,0)-390]+[2*{300-maximum of (9800-9850,0)}] + [Maximum of (9800-10000,0)-230]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9850 | Profit of ₹9,750 | Payoff = [Maximum of (9850-9700,0)-390]+[2*{300-maximum of (9850-9850,0)}] + [Maximum of (9850-10000,0)-230]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9900 | Profit of ₹6,000 | Payoff = [Maximum of (9900-9700,0)-390]+[2*{300-maximum of (9900-9850,0)}] + [Maximum of (9900-10000,0)-230]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9980 | No profit, No loss | Payoff = [Maximum of (9980-9700,0)-390]+[2*{300-maximum of (9980-9850,0)}] + [Maximum of (9980-10000,0)-230]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 9990 | Loss of ₹750 | Payoff = [Maximum of (9990-9700,0)-390]+[2*{300-maximum of (9990-9850,0)}] + [Maximum of (9990-10000,0)-230]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 10000 | Loss of ₹1,500 | Payoff = [Maximum of (10000-9700,0)-390]+[2*{300-maximum of (10000-9850,0)}] + [Maximum of (10000-10000,0)-230]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 11000 | Loss of ₹1,500 | Payoff = [Maximum of (11000-9700,0)-390]+[2*{300-maximum of (11000-9850,0)}] + [Maximum of (11000-10000,0)-230]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 12000 | Loss of ₹1,500 | Payoff = [Maximum of (12000-9700,0)-390]+[2*{300-maximum of (12000-9850,0)}] + [Maximum of (12000-10000,0)-230]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
SHORT CALL BUTTERFLY
| Strategy Details | |
| Strategy Type | Neutral on direction, but bullish on volatility |
| # of legs | 4 (Short 1 Lower Strike Call + Long 2 Middle Strike Calls + Short 1 Higher Strike Call) |
| Maximum Reward | Limited to the extent of net premium received |
| Maximum Risk | Middle Strike Price - Lower Strike Price - Net Premium Received |
| Lower Breakeven Price | Lower Strike Price + Net Premium Received |
| Upper Breakeven Price | Higher Strike Price - Net Premium Received |
| Payoff Calculation | Payoff of lower strike Short Call + (2 * Payoff of middle strike Long Call) + Payoff of higher strike Short Call |
Explanation of the Strategy
A Short Call Butterfly is a strategy that involves writing a lower strike Call, buying two middle strike Calls, and again writing a higher strike Call. The lower strike Call that is written is an ITM Call, the middle strike Calls that are bought are usually ATM Calls, while the higher strike Call that is written is an OTM Call. All these options must belong to the same underlying and must have the same expiration date. Meanwhile, just like in the case of long Call Butterfly, in a short Call Butterfly too, the lower and the higher strike must be equidistant from the middle strike.
This strategy is the opposite of long Call Butterfly. While long Call Butterfly benefits from declining volatility, short Call Butterfly benefits from rising volatility. This is a net credit strategy, in which the maximum profit potential is limited to the extent of net premium received. For the strategy to achieve itsmaximum profit potential, the underlying price will have to either fall below the lower strike price or rise above the higher strike price. For this to happen, volatility is of paramount importance. The higher the volatility, the higher the odds of the underlying price swinging in one or the other direction. So, net-net, it can be said that this strategy is neutral on direction but bullish on volatility.
A Short Call Butterfly has two breakeven points: lower and upper. The trader is in a profitable position as long as the underlying price is either below the lower breakeven point or above the upper breakeven point. On the flip side, if the underlying price consolidates between the two breakeven points, the trader will suffer a loss. Maximum loss under this strategy occurs when the underlying price is exactly at the middle strike. Hence, execute this strategy only when you expect the underlying price to be far off from the middle strikeby expiration.
Benefits of the Strategy
-
This is a net credit strategy, meaning there is no cash outflow at the time of initiation
-
Maximum loss under this strategy is limited
-
This strategy benefits from a surge in volatility
Drawbacks of the Strategy
-
This strategy has limited profit potential
-
The risk reward profile of initiating this strategy is highly unattractive as risk is larger than reward
-
Theta hurts the position when the underlying price is in between the two breakeven points
Strategy Suggestions
-
Ensure that the underlying is trading within a range and you expect this range to hold
-
Within this range trading, have conviction that the underlying will either rise to the upper end of the range or fall to the lower end of the range
-
Execute this strategy when you expect volatility to pick up or when it is already high and is likely to remain so
-
Ensure that the distance between the lower strike and the middle strike is equal to that between the middle strike and the higher strike
-
The spread between the strikes will be a trade-off between risk and reward
-
The wider the difference between the strikes, the higher will be the reward but so would be the risk, and vice versa
-
As the risk involved in trading this strategy is higher than the reward, this strategy must preferably be executed by experienced traders only
-
Because you want the underlying price to move away from the middle strike and becauseyou want volatility to rise, giveyourself sufficient time to go right
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Short Call Butterfly
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to bottom out below zero when the underlying price is near the lower strike and peak out above zero when the underlying price is near the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is positive and is at its highest point at initiation. As the underlying price moves away from the middle strike and approaches either the lower or the higher strike, Gamma tends to move into negative before bottoming out around these extreme strikes. |
| Vega |
Vega is positive and is at its highest point at initiation, meaning the positive impact of a rise in volatility is the greatest at the middle strike. Volatility benefits as long as the position in unprofitable. That said, Vega turns negative when the position becomes profitable, meaning a rise in volatility now starts hurting the position. |
| Theta |
Theta is negative and is at its lowest point at initiation, meaning time decay hurts the most around the middle strike. Time decay hurts the position as long as it is unprofitable. That said, Theta turns positive when the position becomes profitable, meaning time decay now starts benefiting the position. |
Payoff of Short Call Butterfly
The above is the payoff chart of a Short Call Butterfly. Observe that this strategy is profitable outside the two breakeven points. The sweetest spot is when the underlying price is either below the lower strike or above the higher strike. On the other hand, this strategy is unprofitable when the underlying price is between the two breakeven points. See that the maximum loss under this strategy is limited and occurs when the underlying price is exactly at the middle strike.
Example of Short Call Butterfly
Let us say that Mr. ABC expects Nifty to trade within a range but is of the opinion that volatility will pick up soon. Based on this, let us say that he has decided to initiate a short Call Butterfly strategy, wherein he will sell 1 ITM 9500 Call at ₹525, buy 2 ATM 9850 Calls at ₹300 each, and sell 1 OTM 10200 Call at ₹145. Let us summarize the details of the strategy below:
-
Strike price of ITM shortCall = 9500
-
Strike price of ATM longCalls = 9850
-
Strike price of OTM short Call = 10200
-
Quantity of Calls bought = 2 lots (at same strikes)
-
Quantity of Calls sold = 2 lots (at different strike)
-
ShortCall premium (lower strike) = ₹525
-
Long Call premium (middle strike) = ₹300
-
ShortCall premium (higher strike) = ₹145
-
Net Credit = ₹70 (525 + 145 - 2 * 300)
-
Net Credit (in value terms) = ₹5,250 (70 * 75)
-
Lower Breakeven point = 9570 (9500 + 70)
-
Upper Breakeven point = 10130 (10200 - 70)
-
Maximum reward = ₹5,250
-
Maximum risk = ₹21,000 ((9850 - 9500 - 70) * 75)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 8000 | Profit of ₹5,250 | Payoff = [525-Maximum of (8000-9500,0)]+[2*{Maximum of (8000-9850,0)-300}] + [145-Maximum of (8000-10200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9000 | Profit of ₹5,250 | Payoff = [525-Maximum of (9000-9500,0)]+[2*{Maximum of (9000-9850,0)-300}] + [145-Maximum of (9000-10200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9500 | Profit of ₹5,250 | Payoff = [525-Maximum of (9500-9500,0)]+[2*{Maximum of (9500-9850,0)-300}] + [145-Maximum of (9500-10200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9530 | Profit of ₹3,000 | Payoff = [525-Maximum of (9530-9500,0)]+[2*{Maximum of (9530-9850,0)-300}] + [145-Maximum of (9530-10200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9570 | No profit, No loss | Payoff = [525-Maximum of (9570-9500,0)]+[2*{Maximum of (9570-9850,0)-300}] + [145-Maximum of (9570-10200,0)]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither profit nor incur a loss |
| 9700 | Loss of ₹9,750 | Payoff = [525-Maximum of (9700-9500,0)]+[2*{Maximum of (9700-9850,0)-300}] + [145-Maximum of (9700-10200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9850 | Loss of ₹21,000 | Payoff = [525-Maximum of (9850-9500,0)]+[2*{Maximum of (9850-9850,0)-300}] + [145-Maximum of (9850-10200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 10000 | Loss of ₹9,750 | Payoff = [525-Maximum of (10000-9500,0)]+[2*{Maximum of (10000-9850,0)-300}] + [145-Maximum of (10000-10200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 10130 | No profit, No loss | Payoff = [525-Maximum of (10130-9500,0)]+[2*{Maximum of (10130-9850,0)-300}] + [145-Maximum of (10130-10200,0)]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither profit nor incur a loss |
| 10170 | Profit of ₹3,000 | Payoff = [525-Maximum of (10170-9500,0)]+[2*{Maximum of (10170-9850,0)-300}] + [145-Maximum of (10170-10200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 10200 | Profit of ₹5,250 | Payoff = [525-Maximum of (10200-9500,0)]+[2*{Maximum of (10200-9850,0)-300}] + [145-Maximum of (10200-10200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 11000 | Profit of ₹5,250 | Payoff = [525-Maximum of (11000-9500,0)]+[2*{Maximum of (11000-9850,0)-300}] + [145-Maximum of (11000-10200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 12000 | Profit of ₹5,250 | Payoff = [525-Maximum of (12000-9500,0)]+[2*{Maximum of (12000-9850,0)-300}] + [145-Maximum of (12000-10200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
Notice in the above table that maximum profit for this particular case is ₹5,250 and occurs when Nifty is either below the lower strike or above the higher strike. On the other hand, observe that when Nifty is stuck between the two breakeven points, the trader suffers a loss. Maximum loss in case of this example is ₹21,000 and occurs when Nifty is exactly at the middle strike. Another thing to notice for this strategy is the risk to reward ratio. Notice that the risk is four times higher than the possible reward!
Next Chapter
Comments & Discussions in
FYERS Community

Vikash commented on May 29th, 2020 at 4:10 PM
These strategies and all r good however the most important thing to learn in stock market is direction. You should focus more teaching on it.
Abhishek Chinchalkar commented on June 5th, 2020 at 7:36 PM
Hi Vikash, we have covered this in detail in the Technical Analysis module. If you have not yet visited that module, we strongly suggest you to go through it as we have talked about various concepts related to price direction in the TA module.