LONG IRON BUTTERFLY
| Strategy Details | |
| Strategy Type | Neutral on direction, but bullish on volatility |
| # of legs | 4 (Short 1 Lower Strike Put + Long 1 Middle Strike Put + Long 1 Middle Strike Call + Short 1 Higher Strike Call) |
| Maximum Reward | Middle Strike Price - Lower Strike Price - Net Premium Paid |
| Maximum Risk | Limited to the extent of net premium paid |
| Lower Breakeven Price | Middle Strike Price - Net Premium Paid |
| Upper Breakeven Price | Middle Strike Price + Net Premium Paid |
| Payoff Calculation | Payoff of lower strike Short Put+ Payoff of middle strike Long Put + Payoff of middle strike Long Call + Payoff of higher strike Short Call |
Explanation of the Strategy
A Long Iron Butterfly is a strategy that involves selling a lower strike Put, buying a middle strike Put and Call having the same strike price, and selling a higher strike Call. Each of the options must belong to the same underlying and must have the same expiration date. The lower strike Put that is sold is an OTM Put, the higher strike Call that is sold is an OTM Call, while the middle strike Put and Call that are bought are ATM options. A Long Iron Butterfly is a combination of two strategies: Long Straddle and Short Strangle. Do not think much about these strategies for now because we will be talking about each of them in great detail in a later chapter. Alternatively, a Long Iron Butterfly is also a combination of two strategies that we have studied in the past: Bull Call Spread and Bear Put Spread. Meanwhile, an important thing to keep in mind when entering this strategy is that the lower and the higher strike price must be equidistant from the middle strike price.
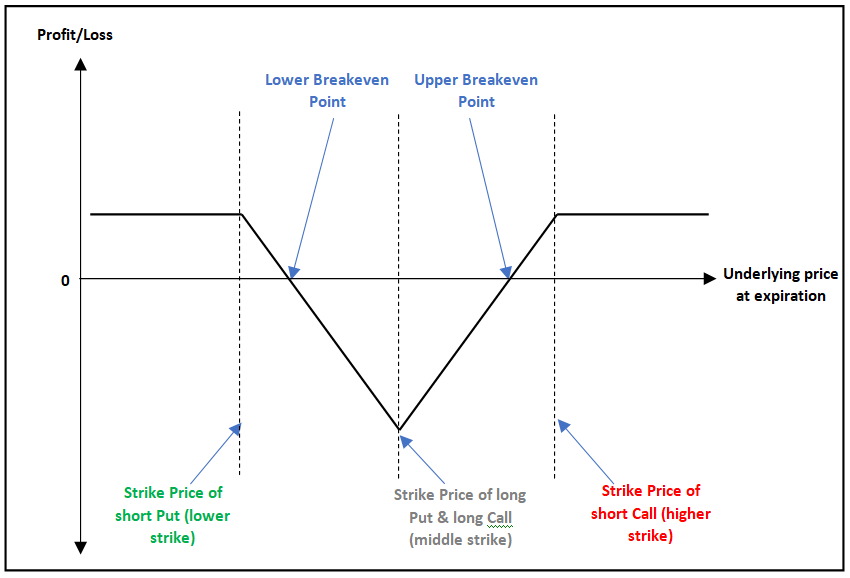
A Long Iron Butterfly is a neutral strategy in terms of direction. This is because this strategy can profit either from a down move in the price of the underlying or from an up move. However, this strategy is bullish on volatility and benefits during times when volatility is rising, and vice versa. This is because the higher the volatility, the higher would be the probability of the position becoming profitable. A Long Iron Butterfly has two breakeven points: lower and upper. The position is unprofitable as long as the underlying price is within the two breakeven points and profitable when the underlying price is outside the two breakeven points. Both profits and losses under this strategy are limited. Maximum profit occurs when the underlying price falls below the lower strike or rises above the higher strike. Similarly, maximum loss occurs when the underlying price is exactly at the middle strike.
As Long Iron Butterfly involves selling OTM options and buying ATM options, this strategy is a net debit strategy. As you will later see, the maximum potential profit under this strategy is usually much smaller than the maximum potential loss. As a result, this strategy must preferably be initiated by experienced option traders only. Before initiating this strategy, one must always take into consideration the risk to reward ratio and must initiate only if this ratio is acceptable and worth trading for. Also, as we shall later see, Long Iron Butterfly has a similar payoff structure as a Short Call Butterfly or a Short Put Butterfly. However, there are differences. The major difference is that short Call/Put Butterfly strategies are net credit strategies, whereas Long Iron Butterfly is a net debit strategy.
Benefits of the Strategy
-
This strategy is direction neutral as the trader can profit from either direction, up or down
-
Maximum loss under this strategy is limited
Drawbacks of the Strategy
-
The cost/risk of this strategy tends to be much greater than the potential reward
-
There are chances that the trader could lose 100% of his net investment
-
When the underlying price is near the middle strike, a decline in volatility would hurt the position
-
A sharp move below the lower strike or above the higher strike would lead to an opportunity loss as maximum profit potential under this strategy is limited
-
Time decay would hurt the trader, especially when the position is unprofitable
Strategy Suggestions
-
See that you have a neutral view on the price direction, but you expect volatility to increase sharply once you have initiated the position
-
Ensure that the distance between the lower strike and the middle strike is equal to that between the middle strike and the higher strike
-
The spread between the strikes will be a trade-off between the cost/risk of the strategy and the reward potential
-
The narrow the difference between the adjacent strikes, the smaller will be the cost and the risk but so would be the reward, and vice versa
-
On the other hand, the narrow the difference between the adjacent strikes, the smaller would be the unprofitable zone, and vice versa
-
As this is a range bound strategy that benefits from rising volatility, ensure that you execute this strategy when expiration is far off, as this would give you sufficient time to go right
-
As the risk/cost tends to be higher than the reward, execute this strategy only when the risk reward ratio is acceptable to you
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Long Iron Butterfly
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to bottom out below zero when the underlying price falls below the lower strike and peak out above zero when the underlying price rises above the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is positive and is at its highest point at initiation. As the underlying price moves away from the middle strike and approaches either the lower or the higher strike, Gamma tends to move into negative before bottoming out around these extreme strikes. |
| Vega |
Vega is positive and is at its highest point at initiation, meaning the positive impact of a rise in volatility is the highest around the middle strike. Volatility benefits as long as the position in unprofitable. That said, Vega turns negative when the position becomes profitable, meaning a rise in volatility now starts hurting the position. |
| Theta |
Theta is negative and is at its lowest point at initiation, meaning time decay hurts the most around the middle strike. Time decay hurts the position as long as it is unprofitable. That said, Theta turns positive when the position becomes profitable, meaning time decay now starts benefiting the position. |
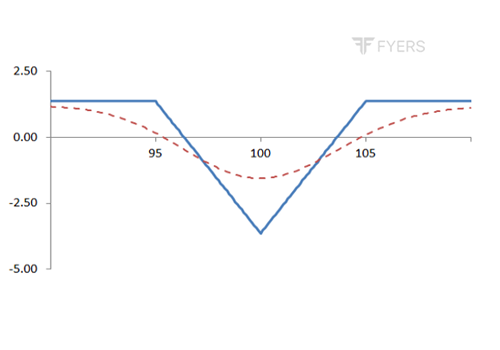
Payoff of Long Iron Butterfly
The above is the payoff chart of a Long Iron Butterfly strategy. Notice that at initiation, this strategy is in the position of maximum loss. As the underlying price starts moving away from the middle strike, the loss starts reducing. Notice that the position is unprofitable as long as the underlying price is within the two breakeven points. It becomes profitable when the underlying price either falls below the lower breakeven point or rises above the upper breakeven point. Maximum profit under this strategy occurs when the underlying price either falls below the lower strike or rises above the higher strike. Meanwhile, maximum loss under this strategy is limited to the extent of net premium that is paid.
Example of Long Iron Butterfly
Let us say that Mr. ABC has looked at the chart of Nifty. He is of the opinion that the index could move in either direction in the short-term, but he expects volatility to pick up going forward. Based on this, let us say that he has decided to initiate a long Iron Butterfly strategy, wherein he will sell 1 OTM 9000 Put at ₹205, buy 1 ATM 9250 Put at ₹310, buy 1 ATM 9250 Call at ₹300, and sell 1 OTM 9500 Call at ₹175. Let us summarize the details of the strategy below:
-
Strike price of OTM shortPut = 9000
-
Strike price of ATM longPut = 9250
-
Strike price of ATM longCall = 9250
-
Strike price of OTM short Call = 9500
-
Short Put premium (lower strike) = ₹205
-
Long Put premium (middle strike) = ₹310
-
Long Call premium (middle strike) = ₹300
-
ShortCall premium (higher strike) = ₹175
-
Net Debit = ₹230 (310 + 300 - 205 - 175)
-
Net Debit (in value terms) = ₹17,250 (230 * 75)
-
Lower Breakeven point = 9020 (9250 - 230)
-
Upper Breakeven point = 9480 (9250 + 230)
-
Maximum reward = ₹1,500 ((9250 - 9000 - 230) * 75)
-
Maximum risk = ₹17,250
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 7000 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-7000,0)]+[Maximum of (9250-7000,0)-310] + [Maximum of (7000-9250,0)-300] + [175-Maximum of (7000-9500,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 8000 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-8000,0)]+[Maximum of (9250-8000,0)-310] + [Maximum of (8000-9250,0)-300] + [175-Maximum of (8000-9500,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9000 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-9000,0)]+[Maximum of (9250-9000,0)-310] + [Maximum of (9000-9250,0)-300] + [175-Maximum of (9000-9500,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9010 | Profit of ₹750 | Payoff = [205-Maximum of (9000-9010,0)]+[Maximum of (9250-9010,0)-310] + [Maximum of (9010-9250,0)-300] + [175-Maximum of (9010-9500,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 9020 | No profit, No loss | Payoff = [205-Maximum of (9000-9020,0)]+[Maximum of (9250-9020,0)-310] + [Maximum of (9020-9250,0)-300] + [175-Maximum of (9020-9500,0)]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 9200 | Loss of ₹13,500 | Payoff = [205-Maximum of (9000-9200,0)]+[Maximum of (9250-9200,0)-310] + [Maximum of (9200-9250,0)-300] + [175-Maximum of (9200-9500,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9250 | Loss of ₹17,250 | Payoff = [205-Maximum of (9000-9250,0)]+[Maximum of (9250-9250,0)-310] + [Maximum of (9250-9250,0)-300] + [175-Maximum of (9250-9500,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9400 | Loss of ₹6,000 | Payoff = [205-Maximum of (9000-9400,0)]+[Maximum of (9250-9400,0)-310] + [Maximum of (9400-9250,0)-300] + [175-Maximum of (9400-9500,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9480 | No profit, No loss | Payoff = [205-Maximum of (9000-9480,0)]+[Maximum of (9250-9480,0)-310] + [Maximum of (9480-9250,0)-300] + [175-Maximum of (9480-9500,0)]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 9490 | Profit of ₹750 | Payoff = [205-Maximum of (9000-9490,0)]+[Maximum of (9250-9490,0)-310] + [Maximum of (9490-9250,0)-300] + [175-Maximum of (9490-9500,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 9500 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-9500,0)]+[Maximum of (9250-9500,0)-310] + [Maximum of (9500-9250,0)-300] + [175-Maximum of (9500-9500,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 10000 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-10000,0)]+[Maximum of (9250-10000,0)-310] + [Maximum of (10000-9250,0)-300] + [175-Maximum of (10000-9500,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 12000 | Profit of ₹1,500 | Payoff = [205-Maximum of (9000-12000,0)]+[Maximum of (9250-12000,0)-310] + [Maximum of (12000-9250,0)-300] + [175-Maximum of (12000-9500,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
In the above table, notice that maximum profit is limited to ₹1,500 and occurs when Nifty is either below the lower strike of 9000 or above the upper strike of 9500. On the other hand, observe that maximum loss is limited to the extent of net premium paid i.e. ₹17,250 and occurs when Nifty is exactly at the middle strike. Notice that the maximum risk for this particular strategy is 11.5 times the maximum reward. This is one of the biggest drawbacks of this strategy - risk tends to be much higher than the reward. Hence, this strategy is primarily meant for professional option traders only.
SHORT IRON BUTTERFLY
| Strategy Details | |
| Strategy Type | Neutral on direction and bearish on volatility |
| # of legs | 4 (Long 1 Lower Strike Put + Short 1 Middle Strike Put + Short 1 Middle Strike Call + Long 1 Higher Strike Call) |
| Maximum Reward | Limited to the extent of net premium received |
| Maximum Risk | Middle Strike Price - Lower Strike Price - Net Premium Received |
| Lower Breakeven Price | Middle Strike Price - Net Premium Received |
| Upper Breakeven Price | Middle Strike Price + Net Premium Received |
| Payoff Calculation | Payoff of lower strike Long Put+ Payoff of middle strike Short Put + Payoff of middle strike Short Call + Payoff of higher strike Long Call |
Explanation of the Strategy
A Short Iron Butterfly is a strategy that involves buying a lower strike Put, selling a middle strike Put and Call having the same strike price, and buying a higher strike Call. Each of these options must have the same underlying and expiration date. The lower strike Put that is bought is an OTM Put, the higher strike Call that is bought is an OTM Call, while the middle strike Put and Call that are sold are ATM options. This strategy is a combination of a Short Straddle and a Long Strangle, each of which would be discussed in the coming chapters. Meanwhile, an important thing to keep in mind when trading this strategy is that the lower and the higher strikes must be equidistant from the middle strike.
A Short Iron Butterfly is a neutral strategy in terms of direction. The trader who initiates this strategy would want the underlying price to consolidate near the middle strike price until expiration. Hence, it can be said that this strategy is bearish on volatility and benefits during times when volatility is reducing. A Short Iron Butterfly has two breakeven points: lower and upper. The position is profitable as long as the underlying price is within the breakeven points and unprofitable when the underlying price is outside the breakeven points. Both profits and losses under this strategy are limited. Maximum profit occurs when the underlying price is exactly at the middle strike, while maximum loss occurs when the underlying either falls below the lower strike or rises above the higher strike.
As Short Iron Butterfly involves buying OTM options and selling ATM options, this strategy is a net credit strategy. In terms of the risk to reward profile, a Short Iron Butterfly is quite attractive. In absolute terms, the maximum potential profit under this strategy is usually much larger than the maximum potential loss. As a result, this strategy can be initiated by intermediate option traders as well. Also, as we shall later see, Short Iron Butterfly has a similar payoff structure as a Long Call Butterfly or a Long Put Butterfly. However, there are differences. The major difference is that Long Call/Put Butterfly strategies are net debit strategies, while Short Iron Butterfly is a net credit strategy.
Benefits of the Strategy
-
This is a net credit strategy
-
The risk of this strategy tends to be much smaller than the potential reward
-
Time decay benefits the position, as long as it is profitable
-
Maximum loss under this strategy is limited
Drawbacks of the Strategy
-
When the underlying price is near the middle strike, a rise in volatility would hurt the position
-
If the underlying price moves outside one of the two breakeven points, the trader will incur a loss
Strategy Suggestions
-
Ensure that you expect the underlying to remain in a range and consolidate near the middle strike
-
Ensure that you have a bearish stance on volatility, and it is likely to reduce once you have initiated the position
-
Ensure that the distance between the lower strike and the middle strike is equal to that between the middle strike and the higher strike
-
The spread between the strikes will be a trade-off between the risk and the reward
-
The wider the difference between the adjacent strikes, the higher will be the risk but so would be the reward, and vice versa
-
Also, the wider the difference between the adjacent strikes, the larger would be the profit making zone, and vice versa
-
As this is a range bound strategy that benefits from falling volatility, ensure that you execute this strategy when there is less time to expiration, as this would give you less time to go wrong
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Short Iron Butterfly
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to peak out above zero when the underlying price is below the lower strike and bottom out below zero when the underlying price is above the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is negative and is at its lowest point at initiation. As the underlying price moves away from the middle strike and approaches either the lower or the higher strike, Gamma tends to move into positive before peaking out around these extreme strikes. |
| Vega |
Vega is negative and is at its lowest point at initiation, meaning the negative impact of a rise in volatility is the highest at the middle strike. Volatility hurts as long as the position in profitable. That said, Vega turns positive when the position becomes unprofitable, meaning a rise in volatility now starts helping the position. |
| Theta |
Theta is positive and is at its highest point at initiation, meaning time decay is most helpful around the middle strike. Time decay benefits the position as long as it is profitable. That said, Theta turns negative when the position becomes unprofitable, meaning time decay now starts hurting the position. |
Payoff of Short Iron Butterfly
The above is the payoff chart of a Short Iron Butterfly strategy. Notice that the strategy is profitable as long as the underlying price is within the confines of the two breakeven point and is unprofitable when the underlying price is either below the lower breakeven or above the upper breakeven. Notice that maximum profit under this strategy occurs when the underlying price is exactly at the middle strike. This profit, however, is limited to the extent of the net premium received. On the other hand, maximum loss under this strategy occurs when the underlying price is either below the lower strike or above the higher strike. In either case, the maximum loss is limited to the extent of the difference between the two adjacent strikes less the net premium received.
Example of Short Iron Butterfly
Let us say that Mr. ABC has looked at the chart of Nifty. He is of the opinion that the index will consolidate near the current level in the short-term with falling bouts of volatility. Based on this, let us say that he has decided to initiate a Short Iron Butterfly strategy, wherein he will buy 1 OTM 9000 Put at ₹205, sell 1 ATM 9250 Put at ₹310, sell 1 ATM 9250 Call at ₹300, and buy 1 OTM 9500 Call at ₹175. Let us summarize the details of the strategy below:
-
Strike price of OTM longPut = 9000
-
Strike price of ATM shortPut = 9250
-
Strike price of ATM shortCall = 9250
-
Strike price of OTM long Call = 9500
-
Long Put premium (lower strike) = ₹205
-
Short Put premium (middle strike) = ₹310
-
Short Call premium (middle strike) = ₹300
-
LongCall premium (higher strike) = ₹175
-
Net Credit = ₹230 (310 + 300 - 205 - 175)
-
Net Credit (in value terms) = ₹17,250 (230 * 75)
-
Lower Breakeven point = 9020 (9250 - 230)
-
Upper Breakeven point = 9480 (9250 + 230)
-
Maximum reward = ₹17,250
-
Maximum risk = ₹1,500 ((9250 - 9000 - 230) * 75)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 7000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-7000,0)-205]+[310-Maximum of (9250-7000,0)] + [300-Maximum of (7000-9250,0)] + [Maximum of (7000-9500,0)-175]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 8000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-8000,0)-205]+[310-Maximum of (9250-8000,0)] + [300-Maximum of (8000-9250,0)] + [Maximum of (8000-9500,0)-175]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-9000,0)-205]+[310-Maximum of (9250-9000,0)] + [300-Maximum of (9000-9250,0)] + [Maximum of (9000-9500,0)-175]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9010 | Loss of ₹750 | Payoff = [Maximum of (9000-9010,0)-205]+[310-Maximum of (9250-9010,0)] + [300-Maximum of (9010-9250,0)] + [Maximum of (9010-9500,0)-175]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 9020 | No profit, No loss | Payoff = [Maximum of (9000-9020,0)-205]+[310-Maximum of (9250-9020,0)] + [300-Maximum of (9020-9250,0)] + [Maximum of (9020-9500,0)-175]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 9200 | Profit of ₹13,500 | Payoff = [Maximum of (9000-9200,0)-205]+[310-Maximum of (9250-9200,0)] + [300-Maximum of (9200-9250,0)] + [Maximum of (9200-9500,0)-175]. As the underlying price at expiration is between the two breakeven points, the trader will earn a profit |
| 9250 | Profit of ₹17,250 | Payoff = [Maximum of (9000-9250,0)-205]+[310-Maximum of (9250-9250,0)] + [300-Maximum of (9250-9250,0)] + [Maximum of (9250-9500,0)-175]. As the underlying price at expiration is between the two breakeven points, the trader will earn a profit |
| 9400 | Profit of ₹6,000 | Payoff = [Maximum of (9000-9400,0)-205]+[310-Maximum of (9250-9400,0)] + [300-Maximum of (9400-9250,0)] + [Maximum of (9400-9500,0)-175]. As the underlying price at expiration is between the two breakeven points, the trader will earn a profit |
| 9480 | No profit, No loss | Payoff = [Maximum of (9000-9480,0)-205]+[310-Maximum of (9250-9480,0)] + [300-Maximum of (9480-9250,0)] + [Maximum of (9480-9500,0)-175]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 9490 | Loss of ₹750 | Payoff = [Maximum of (9000-9490,0)-205]+[310-Maximum of (9250-9490,0)] + [300-Maximum of (9490-9250,0)] + [Maximum of (9490-9500,0)-175]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 9500 | Loss of ₹1,500 | Payoff = [Maximum of (9000-9500,0)-205]+[310-Maximum of (9250-9500,0)] + [300-Maximum of (9500-9250,0)] + [Maximum of (9500-9500,0)-175]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 10000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-10000,0)-205]+[310-Maximum of (9250-10000,0)] + [300-Maximum of (10000-9250,0)] + [Maximum of (10000-9500,0)-175]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 12000 | Loss of ₹1,500 | Payoff = [Maximum of (9000-12000,0)-205]+[310-Maximum of (9250-12000,0)] + [300-Maximum of (12000-9250,0)] + [Maximum of (12000-9500,0)-175]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
In the above table, notice that maximum loss is limited to ₹1,500 and occurs when Nifty is either below the lower strike of 9000 or above the upper strike of 9500. On the other hand, observe that maximum profit is limited to the extent of net premium received i.e. ₹17,250 and occurs when Nifty is exactly at the middle strike of 9250. Notice that this strategy is quite attractive from a risk-reward perspective, as maximum reward for this specific strategy is 11.5 times the maximum risk.
Next Chapter
Comments & Discussions in
FYERS Community