LONG CALL CONDOR
| Strategy Details | |
| Strategy Type | Neutral on direction, but bearish on volatility |
| # of legs | 4 (Long 1 Lower Strike Call + Short 1 Lower Middle Strike Call + Short 1 Higher Middle Strike Call + Long 1 Higher Strike Call) |
| Maximum Reward | Lower Middle Strike Price - Lower Strike Price - Net Premium Paid |
| Maximum Risk | Limited to the extent of Net Premium Paid |
| Lower Breakeven Price | Lower Strike Price + Net Premium Paid |
| Upper Breakeven Price | Higher Strike Price - Net Premium Paid |
| Payoff Calculation | Payoff of lower strike Long Call+ Payoff of lower middle strike Short Call + Payoff of higher middle strike Short Call + Payoff of higher strike Long Call |
Explanation of the Strategy
A Long Call Condor is a strategy wherein the trader would buy 1 lower strike Call, sell 1 lower middle strike Call, sell 1 higher middle strike Call, and buy 1 higher strike Call. Each of the four Calls that are transacted must belong to the same underlying and must have the same expiration date. Usually, the lower strike Call that is bought and the lower middle strike Call that is sold are ITM options, whereas the higher middle strike Call that is sold and the higher strike Call that is bought are OTM options. At the time of strategy initiation, the underlying price is usually somewhere in between the two middle strikes. Usually, all the four options are equidistant from each other. However, this is not a hard and fast rule. In fact, it is not uncommon to see the distance between the lower and the lower middle strike being equal to that between the higher middle and the higher strike, while the distance between the lower middle and the higher middle strike being larger to account for a wider maximum profit zone.
A Long Call Condor is quite similar to a Long Call Butterfly. However, there is an important difference. Recollect that in a Long Call Butterfly, the two middle options that are sold have the same strike price and both these options are usually ATM at the time of initiation. On the other hand, in a Long Call Condor, the two middle options that are sold have different strike prices, usually one being ITM and the other being OTM. Because of this, a Long Call Condor will have a wider maximum profit range, unlike a Long Call Butterfly in which the maximum profit range is restricted to just one point. As a result, an advantage of a Long Call Condor over a Long Call Butterfly is that the former will have a greater probability of earning maximum profit than the latter. That said, this comes at a price. The maximum potential profit for a Long Call Condor is quite smaller than that for a Long Call Butterfly, all else equal. So, there will be a trade-off between a Long Call Condor and a Long Call Butterfly - the former has a wider maximum profit range while the latter has a higher profit in absolute terms.
A Long Call Condor is a range bound strategy, wherein the trader would want the underlying price to consolidate within the confines of the two middle strikes. It naturally follows that once initiated, the trader would want the volatility to decrease, as this would increase the odds of the underlying staying within the two middle strikes. Hence, it can be said that a Long Call Condor is a range bound strategy with a bearish outlook on volatility. Also, as this is a range bound strategy that is already in a profitable position when executed, time decay is beneficial.That said, sometimes this strategy can take a slight directional bias depending on whether the underlying price at initiation is below the two middles strikes (bullish bias) or above the two middle strikes (bearish bias). Meanwhile, just like a Long Call Butterfly, a Long Call Condor is a net debit strategy.
This strategy has two breakeven points. As long as the underlying price is between the two breakeven points, the strategy is profitable. As said earlier, maximum profit under this strategy is limited and occurs when the underlying price is between the two middle strikes. On the other hand, the position becomes unprofitable when the underlying price either falls below the lower breakeven point or rises above the upper breakeven point. Maximum loss under this strategy is limited to the extent of net premium paid and occurs when the underlying price is either below the lower strike or above the higher strike.
Benefits of the Strategy
-
Compared to a Butterfly, this strategy has a wider maximum profit zone
-
Maximum loss is limited no matter how higher or lower the price of the underlying goes
-
The risk reward ratio under this strategy can be extremely attractive
-
Time decay benefits the position as long as it is profitable
-
This strategy has a greater probability of success than a Long Call Butterfly
Drawbacks of the Strategy
-
The wider the maximum profit zone, the higher will be the cost and the potential loss
-
When in a profitable position, an unexpected surge in volatility could be detrimental to the success of the trade
-
Because this strategy involves selling two options, it will require a greater margin in your trading account at the time of initiation
-
A potential to lose the entire net debit amount, in case the underlying falls below the lower strike or rises above the higher strike by expiration
Strategy Suggestions
-
See that your view on the underlying is range bound
-
See that your view on volatility is bearish i.e. you expect volatility to decline going forward
-
Ensure that the strikes are evenly placed. In other words, see that the distance between the lower and the lower middle strike is equal to that between the higher middle and the higher strike
-
However, sometimes, traders keep the distance between the lower middle and the higher middle strikes slightly wider than the other two to account for a larger maximum profit zone
-
The spread between the middle two strikes will be a trade-off between the maximum profit zone and the cost/potential loss of the strategy
-
The wider the spread between the middle strikes, the wider will be the maximum profit zone and the potential profit but so would be the cost as well as the potential loss, and vice versa
-
Because this is a range bound strategy that benefits from declining volatility, ensure that you do not give yourself too much time to go wrong
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Long Call Condor
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to peak out above zero when the underlying price is below the lower strike and bottom out below zero when the underlying price is above the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is negative and is at its lowest point in between the two middle strikes. As the underlying price starts moving away from the midpoint of the two middle strikes and approaches either the lower or the higher strike, Gamma tends to move into positive before peaking out around these extreme strikes. |
| Vega |
Vega is negative and is at its lowest point between the two middle strikes, meaning the negative impact of a rise in volatility is the highest around the middle strikes. Volatility hurts as long as the position in profitable. That said, Vega turns positive when the position becomes unprofitable, meaning a rise in volatility now starts helping the position. |
| Theta |
Theta is positive and is at its highest point between the two middle strikes, meaning time decay is most helpful around the middle strikes. Time decay benefits the position as long as it is profitable. That said, Theta turns negative when the position becomes unprofitable, meaning time decay now starts hurting the position. |
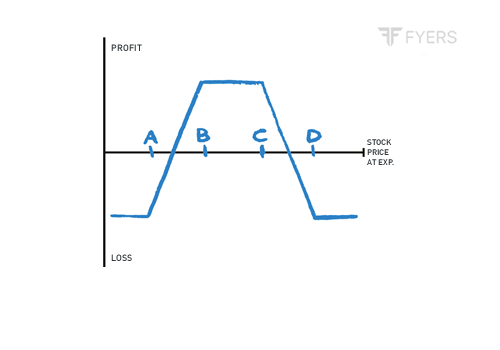
Payoff of Long Call Condor
The above is the payoff chart of a Long Call Condor. Notice that the maximum potential profit under this strategy occurs when the underlying price is within the range of the two middle strike price. On the other hand, notice that the maximum possible loss occurs when the underlying price either falls below the lower strike price or rises above the higher strike price. Both profits and losses under this strategy are limited. Meanwhile, this strategy is in a profitable positions as long as the underlying price is within the confines of the two breakeven points and is unprofitable when the underlying price goes outside either of the two breakeven points.
Example of Long Call Condor
Let us say that Mr. ABC has decided to execute a Long Call Condor strategy on Nifty. The details of the strategy are as below:
-
Strike price of ITM long Call = 8900
-
Strike price of ITM short Call = 9100
-
Strike price of OTM shortCall = 9300
-
Strike price of OTM long Call = 9500
-
LongCall premium (lower strike) = ₹375
-
Short Call premium (lower middle strike) = ₹255
-
Short Call premium (higher middle strike) = ₹165
-
LongCall premium (higher strike) = ₹100
-
Net Debit = ₹55 (375 + 100 - 255 - 165)
-
Net Debit (in value terms) = ₹4,125 (55 * 75)
-
Lower Breakeven point = 8955 (8900 + 55)
-
Upper Breakeven point = 9445 (9500 - 55)
-
Maximum reward = ₹10,875 ((9100 - 8900 - 55) * 75)
-
Maximum risk = ₹4,125
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 7000 | Loss of ₹4,125 | Payoff = [Maximum of (7000-8900,0)-375]+[255-Maximum of (7000-9100,0)] + [165-Maximum of (7000-9300,0)] + [Maximum of (7000-9500,0)-100]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 8000 | Loss of ₹4,125 | Payoff = [Maximum of (8000-8900,0)-375]+[255-Maximum of (8000-9100,0)] + [165-Maximum of (8000-9300,0)] + [Maximum of (8000-9500,0)-100]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 8900 | Loss of ₹4,125 | Payoff = [Maximum of (8900-8900,0)-375]+[255-Maximum of (8900-9100,0)] + [165-Maximum of (8900-9300,0)] + [Maximum of (8900-9500,0)-100]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 8930 | Loss of ₹1,875 | Payoff = [Maximum of (8930-8900,0)-375]+[255-Maximum of (8930-9100,0)] + [165-Maximum of (8930-9300,0)] + [Maximum of (8930-9500,0)-100]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 8955 | No profit, No loss | Payoff = [Maximum of (8955-8900,0)-375]+[255-Maximum of (8955-9100,0)] + [165-Maximum of (8955-9300,0)] + [Maximum of (8955-9500,0)-100]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 9000 | Profit of ₹3,375 | Payoff = [Maximum of (9000-8900,0)-375]+[255-Maximum of (9000-9100,0)] + [165-Maximum of (9000-9300,0)] + [Maximum of (9000-9500,0)-100]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9100 | Profit of ₹10,875 | Payoff = [Maximum of (9100-8900,0)-375]+[255-Maximum of (9100-9100,0)] + [165-Maximum of (9100-9300,0)] + [Maximum of (9100-9500,0)-100]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9200 | Profit of ₹10,875 | Payoff = [Maximum of (9200-8900,0)-375]+[255-Maximum of (9200-9100,0)] + [165-Maximum of (9200-9300,0)] + [Maximum of (9200-9500,0)-100]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9300 | Profit of ₹10,875 | Payoff = [Maximum of (9300-8900,0)-375]+[255-Maximum of (9300-9100,0)] + [165-Maximum of (9300-9300,0)] + [Maximum of (9300-9500,0)-100]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9400 | Profit of ₹3,375 | Payoff = [Maximum of (9400-8900,0)-375]+[255-Maximum of (9400-9100,0)] + [165-Maximum of (9400-9300,0)] + [Maximum of (9400-9500,0)-100]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 9445 | No profit, No loss | Payoff = [Maximum of (9445-8900,0)-375]+[255-Maximum of (9445-9100,0)] + [165-Maximum of (9445-9300,0)] + [Maximum of (9445-9500,0)-100]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 9470 | Loss of ₹1,875 | Payoff = [Maximum of (9470-8900,0)-375]+[255-Maximum of (9470-9100,0)] + [165-Maximum of (9470-9300,0)] + [Maximum of (9470-9500,0)-100]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 9500 | Loss of ₹4,125 | Payoff = [Maximum of (9500-8900,0)-375]+[255-Maximum of (9500-9100,0)] + [165-Maximum of (9500-9300,0)] + [Maximum of (9500-9500,0)-100]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 10000 | Loss of ₹4,125 | Payoff = [Maximum of (10000-8900,0)-375]+[255-Maximum of (10000-9100,0)] + [165-Maximum of (10000-9300,0)] + [Maximum of (10000-9500,0)-100]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 12000 | Loss of ₹4,125 | Payoff = [Maximum of (12000-8900,0)-375]+[255-Maximum of (12000-9100,0)] + [165-Maximum of (12000-9300,0)] + [Maximum of (12000-9500,0)-100]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
In the above table, notice that the maximum profit under this strategy is ₹10,875 and occurs when Nifty is trading between 9100 and 9300. On the other hand, observe that the maximum loss under this strategy is ₹4,125, which is the net debit, and occurs when Nifty is either below 8900 or above 9500. With a maximum possible loss of ₹4,125 and a maximum profit potential of ₹10,875, notice that this strategy has quite a favourable riskreward ratio (the maximum reward is 2.64 times the maximum risk).
SHORT CALL CONDOR
| Strategy Details | |
| Strategy Type | Neutral on direction, but bullish on volatility |
| # of legs | 4 (Short 1 Lower Strike Call + Long 1 Lower Middle Strike Call + Long 1 Higher Middle Strike Call + Short 1 Higher Strike Call) |
| Maximum Reward | Limited to the extent of Net Premium Received |
| Maximum Risk | Lower Middle Strike Price - Lower Strike Price - Net Premium Received |
| Lower Breakeven Price | Lower Strike Price + Net Premium Received |
| Upper Breakeven Price | Higher Strike Price - Net Premium Received |
| Payoff Calculation | Payoff of lower strike Short Call+ Payoff of lower middle strike Long Call + Payoff of higher middle strike Long Call + Payoff of higher strike Short Call |
Explanation of the Strategy
A Short Call Condor is a strategy wherein the trader would sell 1 lower strike Call, buy 1 lower middle strike Call, buy 1 higher middle strike Call, and sell 1 higher strike Call. Each of these options must belong to the same underlying and must have the same expiration date. Usually, but not always, all the four options are equidistant from each other.
Unlike a Long Call Condor, which is a net debit strategy, a Short Call Condor is a net credit strategy. Also, this strategy achieves its maximum profit potential when the underlying price either falls below the lower strike price or rises above the higher strike price. As a result, volatility is of utmost importance to the success of this strategy. The direction in which the underlying price moves is not important. What is however important is that the underlying price swings in either direction (up or down). Hence, it can be said that this strategy is neutral on direction, but bullish on volatility.
Unlike a Short Call Butterfly, in which maximum loss occurs at one point only (the middle strike), a Short Call Condor has a wider maximum loss zone (because the two middle strikes are different). If the underlying price gets stuck between the two middle strikes, the trader will suffer maximum loss under this strategy. Hence, when executing this strategy, the trader must have conviction that the underlying asset will trend up or down and that volatility will increase going forward. Meanwhile, this strategy has two breakeven points, lower and upper. The strategy is unprofitable when the underlying price is within the range of the two breakeven points and is profitable when the underlying price moves outside one of the two breakeven points.
Just like a Short Call Butterfly, a Short Call Condor also has an unattractive risk reward profile as the risk tends to be greater than the potential reward. As a result, this strategy must preferably be executed by experienced option traders only.
Benefits of the Strategy
-
This is a net credit strategy, meaning there is no cash outflow at the time of initiation
-
This strategy works well during times when volatility is expected to rise
-
Maximum loss under this strategy is limited and is known beforehand
Drawbacks of the Strategy
-
Compared to a Butterfly, this strategy has a wider maximum loss zone
-
The risk reward ratio under this strategy is quite unattractive
-
Time decay hurts the position as long as it is unprofitable
-
An unexpected contraction in volatility could be detrimental to the success of the trade
-
Because this strategy involves selling two options, it will require a greater margin in your trading account at the time of initiation
Strategy Suggestions
-
See that your view on the underlying is direction neutral
-
See that you view on volatility is bullish i.e. you expect volatility to increase sharply going forward
-
Ensure that the strikes are evenly placed. In other words, see that the distance between the lower and the lower middle strike is equal to that between the higher middle and the higher strike
-
However, sometimes, traders keep the distance between the lower middle and the higher middle strikes slightly narrow than the other two to account for a smaller maximum loss zone
-
The spread between the two middle strikes will be a trade-off between the maximum loss-making zone and the potential reward of the strategy
-
The wider the spread between the middle strikes, the higher will be the maximum loss-making zone and the maximum possible loss, but so would the maximum possible profit, and vice versa
-
Because this is a direction neutral strategy that benefits from rising volatility, ensure that you give yourself sufficient time to go right
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Short Call Condor
| Greek | Notes |
| Delta |
Delta is at or near zero at initiation. It tends to bottom out below zero when the underlying price is below the lower strike and peak out above zero when the underlying price is above the higher strike. That said, while Delta does become non-zero as the underlying price moves, it does not deviate much from zero. As such, changes in the price of the underlying do not have much impact on this strategy because of the way it is structured. |
| Gamma |
Gamma is positive and is at its highest point in between the two middle strikes. As the underlying price moves away from the midpoint of the two middle strike and approaches either the lower or the higher strike, Gamma tends to move into negative before bottoming out around these extreme strikes. |
| Vega |
Vega is positive and is at its highest point between the two middle strikes, meaning the positive impact of a rise in volatility is the greatestaround the middle strikes. Volatility benefits as long as the position in unprofitable. That said, Vega turns negative when the position becomes profitable, meaning a rise in volatility now starts hurting the position. |
| Theta |
Theta is negative and is at its lowest point between the two middle strikes, meaning time decay hurts the most around the middle strikes. Time decay hurts the position as long as it is unprofitable. That said, Theta turns positive when the position becomes profitable, meaning time decay now starts benefiting the position. |
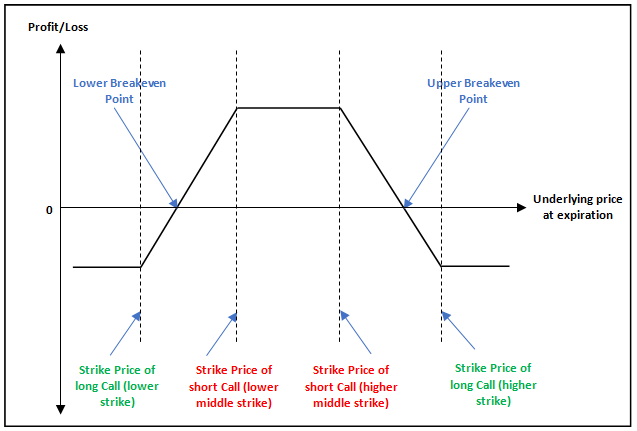
Payoff of Short Call Condor
The above is the payoff chart of a Short Call Condor strategy. Observe that maximum profit under this strategy occurs when the underlying price either falls below the lower strike or rises above the higher strike. On the other hand, see that maximum loss occurs when the underlying price is within the two middle strikes. As the underlying price at initiation is somewhere within the range of the two middle strikes, the trader would want volatility to pick up going forward, so that the probability of the strategy to achieve its maximum profit potential increases.
Example of Short Call Condor
Let us say that Mr. ABC has decided to execute a Short Call Condor strategy on Nifty. The details of the strategy are as below:
-
Strike price of ITM short Call = 8600
-
Strike price of ITM long Call = 8800
-
Strike price of OTM longCall = 9000
-
Strike price of OTM short Call = 9200
-
ShortCall premium (lower strike) = ₹380
-
Long Call premium (lower middle strike) = ₹245
-
Long Call premium (higher middle strike) = ₹145
-
ShortCall premium (higher strike) = ₹70
-
Net Credit = ₹60 (380 + 70 - 245 - 145)
-
Net Credit (in value terms) = ₹4,500 (60 * 75)
-
Lower Breakeven point = 8660 (8600 + 60)
-
Upper Breakeven point = 9140 (9200 - 60)
-
Maximum reward = ₹4,500
-
Maximum risk = ₹10,500 ((8800 - 8600 - 60) * 75)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 7000 | Profit of ₹4,500 | Payoff = [380-Maximum of (7000-8600,0)]+[Maximum of (7000-8800,0)-245] + [Maximum of (7000-9000,0)-145] + [70-Maximum of (7000-9200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 8000 | Profit of ₹4,500 | Payoff = [380-Maximum of (8000-8600,0)]+[Maximum of (8000-8800,0)-245] + [Maximum of (8000-9000,0)-145] + [70-Maximum of (8000-9200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 8600 | Profit of ₹4,500 | Payoff = [380-Maximum of (8600-8600,0)]+[Maximum of (8600-8800,0)-245] + [Maximum of (8600-9000,0)-145] + [70-Maximum of (8600-9200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 8630 | Profit of ₹2,250 | Payoff = [380-Maximum of (8630-8600,0)]+[Maximum of (8630-8800,0)-245] + [Maximum of (8630-9000,0)-145] + [70-Maximum of (8630-9200,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 8660 | No profit, No loss | Payoff = [380-Maximum of (8660-8600,0)]+[Maximum of (8660-8800,0)-245] + [Maximum of (8660-9000,0)-145] + [70-Maximum of (8660-9200,0)]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 8700 | Loss of ₹3,000 | Payoff = [380-Maximum of (8700-8600,0)]+[Maximum of (8700-8800,0)-245] + [Maximum of (8700-9000,0)-145] + [70-Maximum of (8700-9200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 8800 | Loss of ₹10,500 | Payoff = [380-Maximum of (8800-8600,0)]+[Maximum of (8800-8800,0)-245] + [Maximum of (8800-9000,0)-145] + [70-Maximum of (8800-9200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 8900 | Loss of ₹10,500 | Payoff = [380-Maximum of (8900-8600,0)]+[Maximum of (8900-8800,0)-245] + [Maximum of (8900-9000,0)-145] + [70-Maximum of (8900-9200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9000 | Loss of ₹10,500 | Payoff = [380-Maximum of (9000-8600,0)]+[Maximum of (9000-8800,0)-245] + [Maximum of (9000-9000,0)-145] + [70-Maximum of (9000-9200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9100 | Loss of ₹3,000 | Payoff = [380-Maximum of (9100-8600,0)]+[Maximum of (9100-8800,0)-245] + [Maximum of (9100-9000,0)-145] + [70-Maximum of (9100-9200,0)]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 9140 | No profit, No loss | Payoff = [380-Maximum of (9140-8600,0)]+[Maximum of (9140-8800,0)-245] + [Maximum of (9140-9000,0)-145] + [70-Maximum of (9140-9200,0)]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 9170 | Profit of ₹2,250 | Payoff = [380-Maximum of (9170-8600,0)]+[Maximum of (9170-8800,0)-245] + [Maximum of (9170-9000,0)-145] + [70-Maximum of (9170-9200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 9200 | Profit of ₹4,500 | Payoff = [380-Maximum of (9200-8600,0)]+[Maximum of (9200-8800,0)-245] + [Maximum of (9200-9000,0)-145] + [70-Maximum of (9200-9200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 10000 | Profit of ₹4,500 | Payoff = [380-Maximum of (10000-8600,0)]+[Maximum of (10000-8800,0)-245] + [Maximum of (10000-9000,0)-145] + [70-Maximum of (10000-9200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 12000 | Profit of ₹4,500 | Payoff = [380-Maximum of (12000-8600,0)]+[Maximum of (12000-8800,0)-245] + [Maximum of (12000-9000,0)-145] + [70-Maximum of (12000-9200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
In the above table,see that maximum profit under this strategy occurs at extremes, i.e. when Nifty moves either below the lower strike of 8600 or above the higher strike of 9200. On the other hand, maximum loss under this strategy occurs when Nifty gets stuck between the two middle strikes of 8800 and 9000. Hence, the trader who initiates this strategy would want Nifty to move outside one of these middle strikes, irrespective of direction. Meanwhile, for this strategy, the two breakeven points are at 8660 and 9140. The position is loss-making as long as Nifty is trading between these two points and is profitable when Nifty is trading outside one of the two points. Also see that with a maximum possible reward of ₹4,500 and a maximum possible loss of ₹10,500, the risk reward ratio for this strategy is quite unattractive, as maximum risk is 2.3 times the maximum reward.
Next Chapter
Comments & Discussions in
FYERS Community
.PNG)