LONG CALL
| Strategy Details | |
| Strategy Type | Bullish |
| # of legs | 1 |
| Maximum Reward | Unlimited |
| Maximum Risk | Limited to the extent of Call premium paid |
| Breakeven Price | Strike price + Call premium paid |
| Payoff Calculation | Maximum of (Underlying price - Strike Price, 0) - Call premium |
Explaination of the Strategy
This is the most basic and the most popular of all Option strategies. Buying a Call option on an underlying gives the option buyer the right, but not an obligation, to buy the underlying asset at a specified price, called the strike price, on the expiration date. Because a Call option gives the buyer the right to buy the underlying at the strike price, it naturally follows that a Call buyer benefits when the underlying price goes up and above the breakeven price. In fact, the higher the underlying price goes above the breakeven price, the more profitable the trade becomes to the buyer of a Call.
Benefits of the Strategy
-
It is a very simple strategy, as it involves only one leg
-
Limited risk, no matter how lower the underlying goes below the strike price
-
Unlimited profit potential
-
Akin to buying the underlying outright, but at a fraction of the cost
Drawbacks of the Strategy
-
Limited lifespan of Call option
-
Theta works against the Call buyer
-
If the underlying does not rise, there is a risk that the buyer might lose the entire premium
Moneyness of the Strategy
| If… | Option is… |
| Strike Price < Underlying Price | ITM |
| Strike Price = Underlying Price | ATM |
| Strike Price > Underlying Price | OTM |
Strategy Suggestions
-
Ensure that there is a clear upward trajectory in the price of the underlying asset or that the underlying is breaking out of a consolidation zone
-
Ensure that there is sufficient time for the strategy to work out in your favour
-
If there is limited time, the buyer must have strong conviction that the underlying will rise quickly
-
Keep in mind that Theta will decay rapidly during the last few days of the life of the Call option
-
When buying a weekly Call option, avoid buying a Call that is notably OTM. Rather go with an ATM or ITM Call
-
When buying a monthly Call option, avoid buying a deep OTM Call unless you are convinced that it will move ITM well inside the last few days of the option life
-
Ensure that there is sufficient liquidity in the option in which you want to create a position
Option Greeks for long Call position
| Greek | Value is | Notes |
| Delta | Positive | Because Delta is positive, a 1pt rise in the underlying price causes the Call premium to rise by the value of Delta, and vice versa. The larger the Delta, the larger is the impact on Call price. Delta tends to be close to 0 for deep OTM Calls, around 0.5 for ATM Calls, and close to 1 for deep ITM Calls. Also, Delta tends to be at its steepest angle for Calls that are ATM, meaning this is the region when the Call price is most sensitive to changes in underlying price. |
| Gamma | Positive | Because Gamma is positive, a 1pt rise in the underlying price causes Delta to rise by the value of Gamma, and vice versa. The larger the Gamma, the larger is the impact on Delta for a given change in the underlying price. Gamma tends to be at its peak when the Call is ATM and starts tapering as the Call starts moving away from being ATM. Gamma tends to fall to 0 when a Call moves deep ITM/OTM. |
| Vega | Positive | Because Vega is positive, rising IVs have a positive impact on Call price, and vice versa. Vega tends to be at its peak when the Call is ATM and starts tapering off as the Call starts moving away from being ATM. Vega tends to very low for Calls that are deep ITM/OTM.What this all means is that, in magnitude terms, ATM Calls are more sensitive to changes in IVs than are ITM/deep ITM or OTM/deep OTM Calls. Also, the larger the changes in IVs, the more will be the impact of Vega on Call premiums, and vice versa. |
| Theta | Negative | Because Theta is negative, Call pricesare negatively impacted by the passage of time. The longer the time to expiration, the lesser will be the impact of Theta on Call price each day, and vice versa. In the last few days of a Call’s life, absolute Theta rises exponentially, causing the Call to lose its value at a rapid pace. This is especially true for ATM Calls, which have the highest Theta. Hence, closer to expiry, avoid buying ATM Calls. Meanwhile, as ITM Calls are mostly composed of intrinsic value and as OTM Calls have less time value (as they have a low probability of expiring ITM), Theta does not have as much an impact on ITM/OTMCalls as it does on ATM Calls. |
| Rho | Positive | Because Rho is positive, a rise in interest rates benefits the Call buyer, and vice versa. However, this is the least significant of the five Greeks, because it has the least impact on the price of a Call option. |
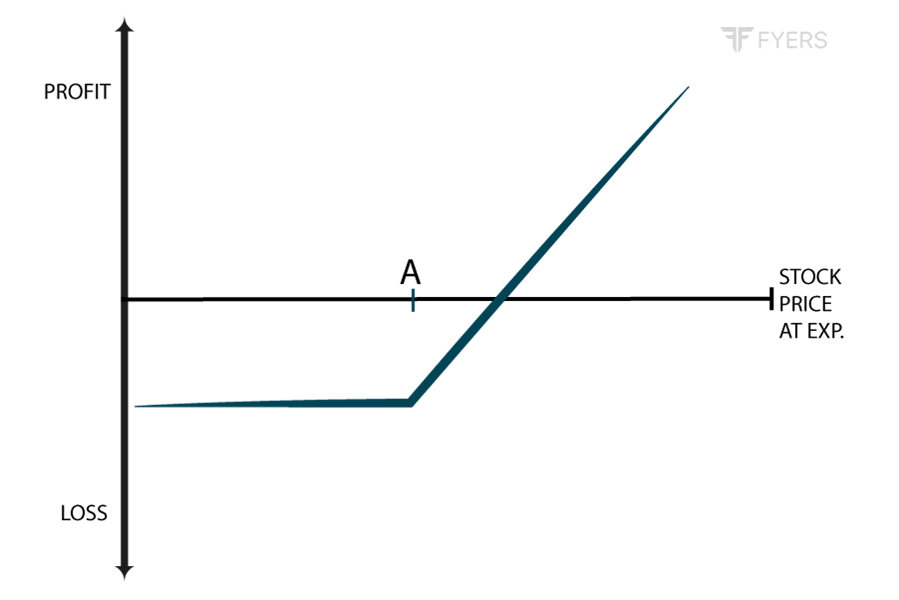
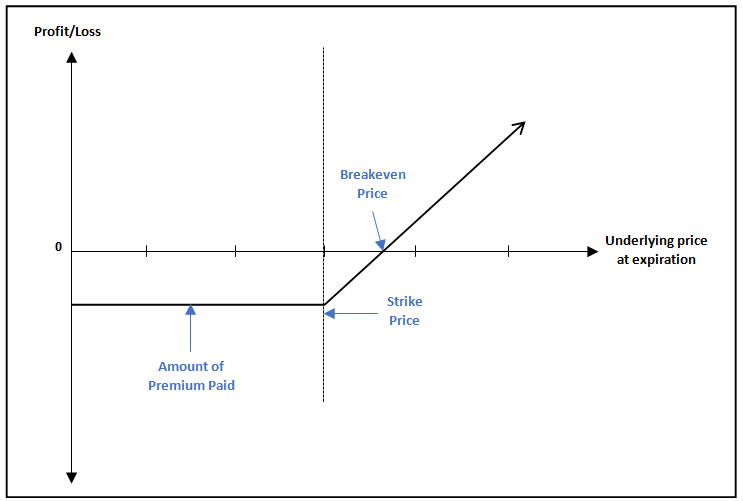
Payoff Chart for long Call position
The above chart shows the payoff stricture for a long Call option. Observe that as long as the underlying price is below the strike price (the dotted vertical line), the option is losing money to the extent of premium that has been paid. When the underlying price is between the strike price and the breakeven price, the losses start reducing. Finally, once the underlying price crosses above the breakeven price, the buyer will start making profits. As can be seen, the profit potential is unlimited in case of a long Call option, because that there is no upper limit up to which the underlying price can go. That said, no matter how lower the underlying price drops, the maximum that the buyer stands to lose is the premium paid upfront.
Example:
Let us assume that Nifty is currently trading at 12000 and has just broken out a resistance after having repeatedly tested the 11900 support. Based on this, I expect the Nifty to rally towards 12300 as long as it is trading above 11900. Hence, I decide to buy a Call option on Nifty. Let us assume that I decide to buy the monthly ATM call option having a strike price of 12000 at a premium of ₹100. Given that Nifty has a lot size of 75, the total premium that I will have to pay to buy the Call option is ₹7,500 (₹100 * 75). Hence, I purchase the 12000 Nifty CE by paying a total of ₹7,500.
-
Strike price = 12000 CE
-
Underlying price = 12000
-
Call Premium = ₹100
-
Call Premium value = ₹7,500
-
Breakeven price of this Call option = 12100 (12000+100)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
|
Underlying price on Expiration |
Net Profit/Loss | Notes |
| 11500 | Loss of ₹7,500 | Because the option is OTM, I will let it expire worthless. In this case, the maximum loss that I suffer is the premium value of ₹7,500 |
| 11900 | Loss of ₹7,500 | Because the option is OTM, I will let it expire worthless. In this case, the maximum loss that I suffer is the premium value of ₹7,500 |
| 12000 | Loss of ₹7,500 | Because the option is ATM, I will be indifferent whether I choose to exercise the option or not. In any case, I would still end up losing the premium value i.e. ₹7,500 |
| 12050 | Loss of ₹3,750 | Because the option is ITM, I will exercise the Call. However, because I have paid a higher premium, I would still end up losing a part of my premium, amounting ₹3,750 ((12050-12000-100)*75) |
| 12200 | Profit of ₹7,500 | Because the option is ITM, I will exercise the Call. In this case, my profit would be ₹7,500 ((12200-12000-100)*75) |
| 12300 | Profit of ₹15,000 |
Because the option is ITM, I will exercise the Call. In this case, my profit would be ₹15,000 ((12300-12000-100)*75) |
| 12500 | Profit of ₹30,000 | Because the option is ITM, I will exercise the Call. In this case, my profit would be ₹30,000 ((12500-12000-100)*75) |
As we can see from the above table, no matter how much the price of the underlying drops, the maximum loss that can be incurred is limited to the extent of premium that is paid upfront. On the other hand, the higher the underlying price goes above the breakeven price, the higher would be the profits that a Call buyer would earn. Notice that losses start reducing when the underlying price is between the strike price and the breakeven price.
Short Call
| Strategy Details | |
| Strategy Type | Bearish |
| # of legs | 1 |
| Maximum Reward | Limited to the extent of Call premium received |
| Maximum Risk | Unlimited |
| Breakeven Price | Strike price + Call premium received |
| Payoff Calculation | Call Premium - Maximum of (Underlying price -Strike price, 0) |
Explanation of the Strategy
This is the opposite of buying a Call option. In this case, the seller will write a Call option, for which he will receive a premium. By selling the Call option, the seller is obliged to honour the contract, in case the buyer exercises his or her right to the contract on expiration. This is a very simple strategy. However, be warned that selling an option is highly risky, especially when one sells a naked Call. This is because while the profit is limited to the extent of premium received, the losses are potentially unlimited. The seller would want the underlying price to stay/fall and stayat or below the strike price. On the flip side, the moment the underlying price crosses above the breakeven price, the seller will start incurring losses. The higher the underlying price goes above the breakeven price, the larger and larger will a seller’s losses get.
Meanwhile, notice the payoff calculation in the table above. Maximum profit to a seller occurs when the underlying price is less than or equal to the strike price, because it enables the seller to keep the entire premium.
Benefits of the Strategy
-
It is a very simple strategy, as it involves only one leg
-
Can generate regular income, if traded well
-
The seller can benefit even if the underlying price remains sideways
-
Theta works in favour of the Call writer
Drawbacks of the Strategy
-
Potential for unlimited losses
-
Maximum reward is limited to the extent of premium received
Moneyness of the Strategy
| If… | Option is… |
| Strike Price < Underlying Price | ITM |
| Strike Price = Underlying Price | ATM |
| Strike Price > Underlying Price | OTM |
Strategy Suggestions
-
Ensure that the trend of the underlying instrument is clearly down or is rangebound with a negative bias or that there is a strong resistance beyond which the underlying is unable to sustain
-
Ensure that the life of the option is short, so that there is less potential for a sustained price rally
-
Keep in mind that Theta will work in seller’s favour during the last few days of the Call option, so this is a big advantage
-
When writing a Call option, ensure that you write an ATM Call, or better yet,a slightly OTM Call
-
Avoid writing an ITM Call option, unless you are extremely bearish on the underlying
-
Avoid writing a Call unless you have bearish view on volatility too, as rising volatility can hurt the short option position
-
Ensure that there is sufficient liquidity in the option in which you want to create a short position
Option Greeks for short Call position
| Greek | Value is | Notes |
|
Delta |
Negative |
Because Delta is negative, a rise in the underlying price hurts the Call writer, and vice versa. A deep ITM Call has Delta closer to -1, while a deep OTM Call has Delta closer to 0. The lower the absolute Delta, the better it is for the Call writer, and vice versa. This is completely logical because a lower Delta makes the Call premium less responsive to changes in the underlying price, which is exactly what the seller wants. A seller must keep a close eye on his/her position when the absolute Delta moves above 0.5. This is because at this juncture, the Delta tends to be at its steepest angle, meaning the Call premium becomes very sensitive to changes in the underlying price and could rise sharply if the underlying price moves higher, a situation that a seller wouldn’t want to be into. |
| Gamma | Negative |
Because Gamma is negative, a high Gamma value can hurt a call writer, especially if the underlying price moves above the strike price. As Gamma tends to be at its peak for a Call that is ATM and starts tapering off as the Call moves away from being ATM, a seller would benefit as the Call moves from ATM to OTM, because the absolute Delta will move below 0.5 and the Gamma will start reducing, meaning its impact on Delta will start tapering off. |
| Vega | Negative |
Because Vega is negative, rising IVs hurt the Call writer, and vice versa. This is because rising IVs cause the Call premiums to rise, which is not what the seller would want. Instead, the seller would want the IVs to reduce, as this would lower the Call premium. |
| Theta | Positive |
Theta is the Call seller’s best friend. It is positive, meaning that the passage of time causes the Call premium to reduce, all else equal. |
| Rho | Negative |
Because Rho is negative, a rise in interest rates hurts the Call seller, and vice versa. However, this is the least significant of the five Greeks, because it has the least impact on the price of a Call option, especially ones that are shorter-dated. |
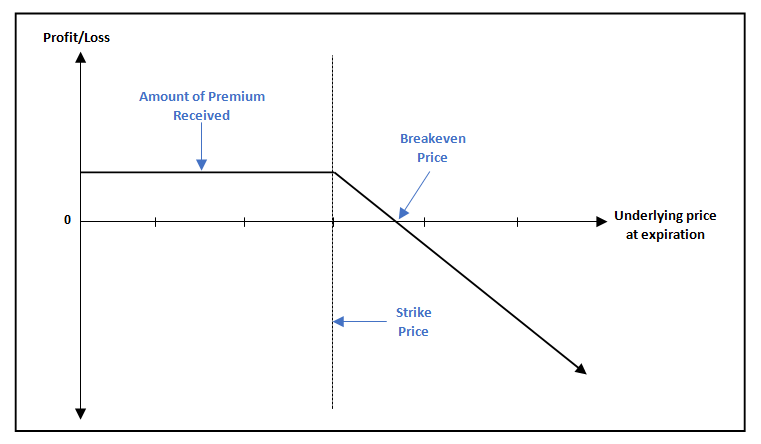
Payoff Chart for short Call position
The above chart shows the payoff stricture for a short Call option. Observe that as long as the underlying price is at or below the strike price (the dotted vertical line), the seller gets to keep the entire premium that he or she has received from the buyer. Once the underlying price crosses above the strike price, the seller’s profit will start reducing until the underlying price reaches the breakeven price. And once the underlying price crosses above the breakeven price, the seller will start making losses. Observe that the higher the underlying price goes above the breakeven price, the higher will be the seller’s losses. In fact, given that there is no upper limit up to which the underlying price can go, it is worth mentioning that the seller’s losses could get theoretically unlimited. Hence, unless hedged, a short Call can be a very risky strategy if not properly managed.
Example :
Let us assume that Nifty is currently trading at 11990 and has been unable to move past the 12000 hurdle despite multiple attempts. Let us also assume that the price momentum is now starting to show signs of weakening. Based on this, I expect the Nifty to stay in a range between11800to 12000 in the coming few days and exhibit a weaker price trend within this range. Hence, I decide to sell a Call option on Nifty. Let us assume that I decide to sell the monthly ATM Call having a strike price of 12000 for a premium of ₹110. Given that Nifty has a lot size of 75, the total premium that I will receive to sell the Call option is ₹8,250 (₹110 * 75). Hence, I write the 12000 Nifty CE and receive a total of ₹8,250.
-
Strike price = 12000 CE
-
Underlying price = 11990
-
Call Premium = ₹110
-
Call Premium value = ₹8,250
-
Breakeven price of this Call option = 12110 (12000+110)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
|
Underlying price on Expiration |
Net Profit/Loss |
Notes |
|
13000 |
Loss of ₹66,750 |
As this option is expiring ITM, the buyer will exercise his right to buy the underlying at 12000. In this case, the seller will suffer a loss of ₹66,750((110- 13000+12000)*75) |
|
12500 |
Loss of ₹29,250 |
As this option is expiring ITM, the buyer will exercise his right to buy the underlying at 12000. In this case, the seller will suffer a loss of ₹29,250((110- 12500+12000)*75) |
|
12300 |
Loss of ₹14,250 |
As this option is expiring ITM, the buyer will exercise his right to buy the underlying at 12000. In this case, the seller will suffer a loss of ₹14,250((110- 12300+12000)*75) |
|
12100 |
Profit of ₹750 |
As this option is expiring ITM, the buyer will exercise his right to buy the underlying at 12000. However, as the premium received exceeds the difference between the underlying price and the strike price, the seller will still make a gain to the tune of ₹750((110- 12100+12000)*75) |
|
12050 |
Profit of ₹4,500 |
As this option is expiring ITM, the buyer will exercise his right to buy the underlying at 12000. However, as the premium received exceeds the difference between the underlying price and the strike price, the seller will still make a gain to the tune of ₹4,500((110- 12050+12000)*75) |
|
12000 |
Profit of ₹8,250 |
Because the option is ATM, the buyer will indifferent in terms of whether he or she exercises it. Either ways, the seller will get to keep the entire premium amount of ₹8,250((110- 12000+12000)*75) |
|
11900 |
Profit of ₹8,250 |
Because the option is OTM, the buyer will not exercise the option. Hence, the seller will get to keep the entire premium amount of ₹8,250 |
|
11500 |
Profit of ₹8,250 |
Because the option is OTM, the buyer will not exercise the option. Hence, the seller will get to keep the entire premium amount of ₹8,250 |
Observe from the above table that the losses a Call seller can suffer could be huge, depending on how higher the underlying price goes above the breakeven price. On the other hand, the profit potential of a Call seller will be limited to the extent of premium that he or she has received, no matter how lower the underlying price goes below the strike price. Because of this limited reward and unlimited risk potential, a short Call, especially one without any form of protection such as a hedge, should be initiated only by experienced traders and those who have sufficient margin in their trading account. Also, one should initiate this strategy only if one has a strong conviction that the underlying price will stay below the breakeven price (preferably at or below the strike price) until expiry or until the time the position is held onto.
Trade-off between Greeks when selecting Strikes
When buying a Call option, a trader needs to take into consideration his/her perception about each Greek. Keep in mind that buying a Call is not just about the direction (Delta), but also about other factors such as Theta, Vega, and Gamma. Depending on a combination of these factors, the type of strike price that is chosen can vary. Let us see how:
Playing for direction only (Delta)
If the main objective is to play for direction only and to replicate movements that are similar to those of the underlying asset itself, then one can consider buying a deep ITM Call. This is because such options have a high Delta (usually upwards of 0.85), making them highly responsive to a rise in the underlying price. Furthermore, a Call that is deep ITM will have very less time value, making it hardly responsive to other Greeks (Gamma, Vega, and especially Theta). Because of this, unlike an ATM or OTM strike, a deep ITM strike would give the buyer more leeway should the underlying price not move as expected for a brief period of time, such as becoming sideways or declining a little for a short span before resuming its up move. Having said that, there is a trade-off in buying deep ITM Calls. High Delta value means the Call premium will also fall sharply in case the forecast goes wrong and there is a sharp decline in the price of the underlying.
Playing for volatility too (Vega)
If the buyer is bullish on volatility, he or she can increase his/her volatility exposure by buying an option that has a higher Vega, such as buying an ATM option (remember, Vega tends to be at its peak when an option is ATM). However, the trade-off here is that an ATM Call will also have the highest Theta, and hence will be subject to maximum time erosion, in case the underlying price does not move much. Alternatively, if the buyer expects the volatility to decrease, he or she can decrease his/her volatility exposure by buying an option that has a lower Vega, such as buying an ITM or an OTM option. Again, this comes with a trade-off. If the underlying price falls sharply, an ITM Call could lose its value at a rapid pace till it moves towards being ATM; whereas, an OTM Call will have lower exposure to Delta, meaning the underlying will have to rise substantially, for the option premium to become more and more responsive to changes in the underlying price.
Minimizing the impact of Time Decay (Theta)
What if the underlying price rises, but at a slower than expected pace? In this case, a portion of the rise in Call premium could be eaten up by the effects of time decay i.e. Theta. Sometimes, the negative impact of time decay can more than offset the positive impact of the rise in the underlying price. Hence, if the buyer is of the opinion that the underlying will rise but is not so sure as to how long it will take for the rally to materialize within the option’s life, he or she could reduce the Theta exposure by buying an ITM or OTM Call. However, these will come with trade-offs, as were mentioned earlier. Alternatively, if the buyer is of the view that the underlying price will rise sharply and quickly from the strike price, then Theta becomes less of a concern. In such a case, buying an ATM Call makes sense.
On the other hand, what benefits a Call buyer should logically hurt a Call seller, and vice versa. For instance, while Theta is the buyer’s biggest enemy, it is the seller’s best friend. Similarly, while rising IVs benefit the holder of a Call option, falling IVs benefit the writer of a Call option. And while rising Delta helps a Call buyer as it makes the Call price more responsive to the underlying price, falling Delta benefits a Call writeras it makes the Call premium less responsive to changes in the underlying price.
When you sell a Call option, each of Delta, Gamma, and Vega are negative. This is as good as saying one is short each of these Option Greeks. The risk here is that an adverse move in the underlying price or volatility could severely hurt the short Call position. As an example, for a short Delta position, the risk is of the underlying price rising; while for a short Vega position, the risk is of the volatility expanding. Often, there is a tendency for short Delta and short Vega to act as a partial hedge against one other in a short Call position. This is because of the relationship between the underlying price and volatility. Periods when the underlying price is going up usually causes volatility to contract, whereas periods when the underlying price is declining usually causes volatility to expand. Hence, while a rise in the underlying price hurts the short Call position, it is sometimes offset by a fall in IV. To understand the approximate impact, one will have to closely observe the values of Delta and Vega. Remember, when selling a Call, the objective is to buyback the Call at a lower price, and hence profit from the trade. For this to happen, one must keep a close watch on Delta and Vega, as either of these Greeks could make or break the trade for the seller.
Next Chapter
Comments & Discussions in
FYERS Community
Ravi Guttennavar commented on April 8th, 2020 at 11:31 PM
Hi Tejas
Great Content....
I am regularly look for trading knowledge on internet and i am extremely proud to say that fyers school of stock produces one of best contents...
Your work on explaining chart patterns,indicators,oscillators is unlike any thing i have ever seen on internet.
Keep up the Great Work...
Appreciate the efforts the team has put in.
Shriram commented on April 10th, 2020 at 6:37 PM
Hi Ravi, thank you for such a valuable feedback!