BEAR PUT LADDER
| Strategy Details | |
| Strategy Type | Moderately bearish when initiated, but only upto a certain point |
| # of legs | 3 (Long ATM Put + Short OTM, Middle Strike Put + Short OTM, Lower Strike Put) |
| Maximum Reward | Higher Strike price - Middle Strike price - Net Premium paid |
| Maximum Upside Risk | Limited to the extent of Net Premium Paid, as long as the underlying price is above the higher strike price |
| Maximum Downside Risk | Unlimited, once the underlying price falls below the lower breakeven price |
| Upper Breakeven Price | Higher Strike price - Net Premium paid |
| Lower Breakeven Price | Lower Strike price + Middle Strike price - Higher Strike price + Net Premium paid |
| Payoff Calculation | Payoff of Long Put+ Payoff of middle, Short Put + Payoff of lower, Short Put |
Explanation of the Strategy
A Bear Put Ladder is an extension of a Bear Put Spread, but with a third leg that is added into the picture. Recollect that in a Bear Put Spread, the trader buys one ATM Put and sells one OTM Put. In a Bear Put Ladder, the trader would buy one ATM Put, sell one OTM Put, and again sell one OTM Put with an even lower strike price. The objective of this strategy is two-folds. One is to reduce the overall cost of the strategy, while the other is to lower the upper breakeven point of the strategy. Just to say, this strategy has two breakeven points: upper breakeven point and lower breakeven point. The upper breakeven point is the point below which the underlying price will have to fall for the trader’s net cost to become nil and for the position to eventually start making money. Meanwhile, the lower breakeven point is the point below which the trader would not want the underlying price to fall as this would expose him/her towards incurring unlimited losses.
Instead, the trader would want the underlying price to trade between the two breakeven points, preferably between the middle and the lower strike price. The reason why the trader would want the underlying price to trade and stay within the middle and lower strike price is because it is within this range that the trader’s profit potential is maximum. Bear Put Ladder is an advanced option strategy because it involves selling two Puts as opposed to buying just one Put, because of which the trader would be exposed to unlimited risk and limited reward potential. Under this strategy, there are two types of risk: upside risk and downside risk. Maximum upside risk is limited to the extent of net premium paid. No matter how higher the underlying price rises above the higher strike, the trader would not suffer any more losses than the net premium that he/she had paid upfront. On the other hand, maximum downside risk is potentially unlimited and occurs when the underlying price falls below the lower breakeven point.
Bear Put Ladder is a conservatively bearish strategy. The trader would want the underlying price to decline, but only up to the lower strike price. Because the trader has sold two Puts at lower strikes as opposed to just one Put that is bought at a higher strike, he/she wouldn’t want the underlying price to fall sharply, as this would expose him/her to the likelihood of suffering huge losses. Hence, this strategy must be initiated only when one is conservatively bearish on the underlying and wants to reduce the overall cost of the strategy even further. For the rest of our discussion, we will be assuming that a Bear Put Ladder is a net debit strategy. However, keep in mind that depending on the strikes chosen, this strategy can also be a net credit strategy.
Benefits of the Strategy
-
Because of the second Put that is sold, the overall cost of the strategy comes down
-
Reduces the upper breakeven point of the strategy i.e. brings it closer to the strike price of the Put that is bought
-
The two strikes for shorting the Puts can be chosen depending upon one’s trading preferences
Drawbacks of the Strategy
-
If the underlying falls below the lower breakeven point, losses could be unlimited
-
Because this strategy involves selling two options, it will require a greater margin in your trading account
-
As long as the underlying price is above the upper breakeven point, Theta will work against the trader
Strategy Suggestions
-
Ensure that the trend is moderately bearish, that there is a clear resistance at a higher level which you feel will hold, and that there is a strong support at a lower level which you feel will not break
-
The ratio of Puts bought and sold must be maintained. For instance, if you buy 1 Put, you can sell only 1 Put each of two different strikes (for a total of 2 Puts sold)
-
Do not just randomly choose strikes for the Puts that you want to sell. Instead, select strikes based on your risk-reward profile and based on key pivots visible on the charts
-
Remember, you want the underlying price to fall to at least the middle strike by expiration, so as to earn maximum profit on the strategy
-
The difference between the higher strike and the two lower strikes will be a trade-off between the net cost of the strategy and the reward
-
If the underlying price falls below the lower breakeven point, consider closing out the position if you feel the downside will continue
-
Keep sufficient spread between the higher strike and the lower strike to account for any unexpected sudden decline in the underlying price
-
Because the downside risk is unlimited, see that there is not too much time left in the life of the option contract, as doing so would give you less time to go wrong
-
Ensure that there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Bear Put Ladder
At the time of strategy initiation, the sign of Greeks can vary depending upon the distance between the strike price of the long Put (higher strike) and those of the two short Puts (middle and lower strike). Hence, we shall be talking about Greeks in general without discussing about the sign of each Greek at initiation.
| Greek | Notes |
| Delta |
Because this strategy is bearish at initiation, Delta initially is negative and hence benefits the position when the underlying price falls, and vice versa. However, Delta turns positive as the underlying price continues dropping and inches towards the strikes of the short Puts. As a result, falling prices eventually start hurting the option position. |
| Gamma |
Gamma peaks out at the higher strike, causing the Delta to become more negative if the underlying price falls. However, if the price fall continues, Gamma turns negative, eventually lifting the Delta into positive zone. Gamma bottoms out at the lower strike, causing the Delta to become more positive (albeit at a slower rate) if the underlying price continues falling. |
| Vega |
When the underlying price is above the higher breakeven point or below the lower breakeven point, Vega is positive, because of which rising volatility is helpful to the position, and vice versa. On the other hand, when the underlying price is in between the two breakeven points, Vega is negative, because of which rising volatility hurts the position, and vice versa. |
| Theta |
When the underlying price is above the higher breakeven point or below the lower breakeven point, Theta is negative, because of which time decay hurts the position. On the other hand, when the underlying price is in between the two breakeven points, Theta is positive, because of which time decay benefits the position. |
| Rho |
As Rho is initially negative, rising interest rates can hurt the position, and vice versa. However, once the underlying price falls and moves towards the lower strike price, Rho turns positive because of which rising interest rates start benefiting the position, and vice versa. |
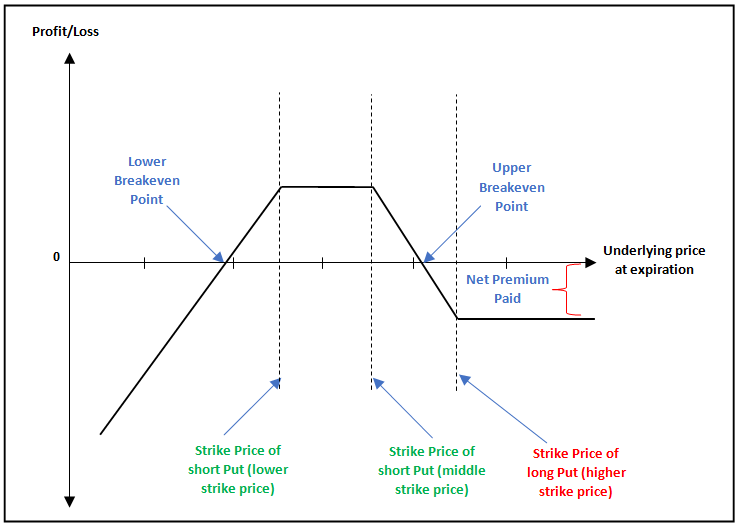
Payoff of Bear Put Ladder
The above chart shows the payoff structure of the Bear Put Ladder strategy. Notice that when the underlying price is above the upper breakeven point, the trader suffers a loss, which is limited to the extent of net premium that is paid upfront. No matter how higher the underlying price rises above the upper breakeven point, the loss does not increase any further. Meanwhile, observe that the trader makes a profit when the underlying price falls below the upper breakeven point. He/she continues making profit as long as the underlying price is above the lower breakeven price. Within this zone, maximum profit is earned when the underlying price is within the range of the middle and the lower strikes. Finally, observe the losses that the trader would suffer once the underlying price falls below the lower breakeven point. These losses are potentially unlimited and can get huge, if the underlying price continues falling and the trader holds on to his/her position. As can be seen, a trader who initiates this strategy would want the underlying price to fall below the upper breakeven point but stay above the lower breakeven point.
Example of Bear Put Ladder
Let us say that Mr. ABC, based on his observations on Nifty, has decided to initiate a Bear Put Ladder strategy, wherein he will buy 1 ATM 9100 Put at ₹400, sell 1 OTM 8500 Put at ₹190 and another OTM 8400 Put at ₹170. Let us summarize the details of the strategy below:
-
Strike price of long Put = 9100
-
Strike price of middle short Put = 8500
-
Strike price of lower short Put = 8400
-
Long Put premium (higher strike) = ₹400
-
Short Put premium (middle strike) = ₹190
-
Short Put premium (lower strike) = ₹170
-
Net Debit = ₹40 (400 - 190 - 170)
-
Net Debit (in value terms) = ₹3,000 (40 * 75)
-
Upper breakeven point = 9060 (9100 - 40)
-
Lower breakeven point = 7840 (8400 + 8500 - 9100 + 40)
-
Maximum upside risk = ₹3,000
-
Maximum downside risk = unlimited
-
Maximum Potential Profit = ₹42,000 ((9100 - 8500 - 40) * 75)
Now, let us assume a few scenarios in terms of where Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 12000 | Loss of ₹3,000 | Payoff = [maximum of (9100-12000,0)-400]+[190- maximum of (8500-12000,0)] + [170- maximum of (8400-12000,0)]. As the underlying price at expiration is above the upper breakeven price, the trader will incur a loss |
| 10000 | Loss of ₹3,000 | Payoff = [maximum of (9100-10000,0)-400]+[190- maximum of (8500-10000,0)] + [170- maximum of (8400-10000,0)]. As the underlying price at expiration is above the upper breakeven price, the trader will incur a loss |
| 9100 | Loss of ₹3,000 | Payoff = [maximum of (9100-9100,0)-400]+[190- maximum of (8500-9100,0)] + [170- maximum of (8400-9100,0)]. As the underlying price at expiration is above the upper breakeven price, the trader will incur a loss |
| 9080 | Loss of ₹1,500 | Payoff = [maximum of (9100-9080,0)-400]+[190- maximum of (8500-9080,0)] + [170- maximum of (8400-9080,0)]. As the underlying price at expiration is above the upper breakeven price, the trader will incur a loss |
| 9060 | No profit, No loss | Payoff = [maximum of (9100-9060,0)-400]+[190- maximum of (8500-9060,0)] + [170- maximum of (8400-9060,0)]. As the underlying price at expiration is equal to the upper breakeven price, the trader will neither make a profit nor incur a loss |
| 8800 | Profit of ₹19,500 | Payoff = [maximum of (9100-8800,0)-400]+[190- maximum of (8500-8800,0)] + [170- maximum of (8400-8800,0)]. As the underlying price at expiration is below the upper breakeven price, the trader will make a profit |
| 8500 | Profit of ₹42,000 | Payoff = [maximum of (9100-8500,0)-400]+[190- maximum of (8500-8500,0)] + [170- maximum of (8400-8500,0)]. As the underlying price at expiration is below the upper breakeven price, the trader will make a profit |
| 8400 | Profit of ₹42,000 | Payoff = [maximum of (9100-8400,0)-400]+[190- maximum of (8500-8400,0)] + [170- maximum of (8400-8400,0)]. As the underlying price at expiration is below the upper breakeven price, the trader will make a profit |
| 8000 | Profit of ₹12,000 | Payoff = [maximum of (9100-8000,0)-400]+[190- maximum of (8500-8000,0)] + [170- maximum of (8400-8000,0)]. As the underlying price at expiration is below the upper breakeven price, the trader will make a profit |
| 7840 | No profit, No loss | Payoff = [maximum of (9100-7840,0)-400]+[190- maximum of (8500-7840,0)] + [170- maximum of (8400-7840,0)]. As the underlying price at expiration is equal to the lower breakeven price, the trader will neither make a profit nor incur a loss |
| 7000 | Loss of ₹63,000 | Payoff = [maximum of (9100-7000,0)-400]+[190- maximum of (8500-7000,0)] + [170- maximum of (8400-7000,0)]. As the underlying price at expiration is below the lower breakeven price, the trader will incur a loss |
| 6000 | Loss of ₹138,000 | Payoff = [maximum of (9100-6000,0)-400]+[190- maximum of (8500-6000,0)] + [170- maximum of (8400-6000,0)]. As the underlying price at expiration is below the lower breakeven price, the trader will incur a loss |
| 5000 | Loss of ₹213,000 | Payoff = [maximum of (9100-5000,0)-400]+[190- maximum of (8500-5000,0)] + [170- maximum of (8400-5000,0)]. As the underlying price at expiration is below the lower breakeven price, the trader will incur a loss |
It can be seen from the above table that maximum upside loss is limited to the extent of ₹3,000 no matter how higher Nifty goes above 9100, while downside loss is potentially unlimited and gets higher and higher as Nifty drops lower and lower below 7840. It can also be seen that the trader profits when Nifty is in between the two breakeven points of 7840 and 9060. The sweetest spot of the strategy occurs when Nifty is between the middle and the lower strike of 8500 and 8400 respectively, as this enables the trader to earn maximum profit on the strategy, which is ₹42,000.
BULL PUT LADDER
| Strategy Details | |
| Strategy Type | Sideways to moderately bullish when initiated, but bearish after a certain point |
| # of legs | 3 (Short slightly OTM, Higher Strike Put + Long OTM, Middle Strike Put + Long OTM, Lower Strike Put) |
| Maximum Downside Reward | Potentially unlimited |
| Maximum Upside Reward | Limited to the extent of net premium received |
| Maximum Risk | Limited to the extent of higher strike price - middle strike price - Net premium received |
| Upper Breakeven Price | Higher Strike price - Net Premium received |
| Lower Breakeven Price | Lower Strike price + Middle Strike price - Higher Strike price + Net Premium received |
| Payoff Calculation | Payoff of higher short Put + Payoff of middle long Put + Payoff of lower long Put |
Explanation of the Strategy
A Bull Put Ladder is an extension of a Bull Put Spread. However, instead of having 2 legs, a Bull Put Ladder has three legs. This strategy involves writing an ATM or slightly OTM Put option having a higher strike price, buying the same number of OTM Put option having a middle strike price, and again buying the same number of OTM Put option but having a lower strike price. Because this strategy involves buying two Puts as opposed to selling just one Put, the trader is essentially net long, which enables him/her to earn unlimited profit once the underlying price fall below a certain price level. That said, assuming the strategy implemented is a net credit strategy, a trader would retain the net premium that he/she has received if the underlying price stays above the higher strike price by expiration. Note the usage of the word ‘assuming’ in the previous sentence. We have said this because this strategy can be either a net debit or a net credit strategy. For the rest of our discussion, we will assume the strategy to be a net credit strategy.
A Bull Put Ladder has two breakeven points: upper and lower. As long as price is above the upper breakeven point, the trader will be in a profitable position as he/she will get to retain the entire or some portion of the net premium received. Meanwhile, the lower breakeven point is a point below which the trader would have the potential to earn unlimited profits. In between the two breakeven points is the loss zone. The maximum loss under this strategy is limited and occurs when the underlying price is in between the middle and the lower strike price. As this is a net credit strategy, it can be said that this strategy is neutral to slightly bullish when initiated. This is because, assuming the Put sold is slightly OTM, the trader gets to keep the entire net premium as long as the underlying price is above the higher strike price. However, below a certain level (i.e. the lower strike price), this strategy turns bearish as the position benefits more and more the deeper the underlying price drops below the lower breakeven price.
Benefits of the Strategy
-
Potential for unlimited profit if the underlying price plummets below the lower breakeven point
-
Potential to retain the entire net premium if the underlying price stays above the higher strike
-
The strategy is subject to limited risk
Drawbacks of the Strategy
-
If the underlying price gets stuck between the two breakeven points, the trader will suffer a loss
-
If the underlying price stays between the middle and the lower strike, the trader will suffer the maximum loss under this strategy
-
Sometimes, the strategy could be a net debit strategy
Strategy Suggestions
-
The ratio of Puts bought and sold must be maintained. For instance, if you sell 1 Put, you can buy only 1 Put each of two different strikes (for a total of 2 Puts bought)
-
When choosing the two strikes for buying the Puts, do not just randomly select any strike. Remember, if the underlying price declines, you would want it to fall below the lower breakeven point. Hence, choose the long Put strikes accordingly
-
The difference between the higher strike and the two lower strikes will be a trade-off between net premium received and risk
-
The larger the difference between the higher strike and the two lower strikes, the larger would be the net premium received but so would be the risk, and vice versa
-
Because this strategy involves buying two Puts and attains its maximum profit potential once the underlying declines below the lower breakeven point, see that there is sufficient time left in the life of the option contract, for the strategy to work in your favour
-
Ensure that there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Bull Put Ladder
At the time of strategy initiation, the sign of Greeks can vary depending upon the distance between the strike price of the short Put (higher strike) and those of the two long Puts (middle and lower strike). Hence, we shall be talking about Greeks in general without discussing about the sign of each Greek at initiation.
| Greek | Notes |
| Delta |
Because this strategy is neutral to bullish at initiation, Delta initially is positive and hence benefits the position when the underlying price rises, and vice versa. However, Delta turns negative when the underlying price drops and inches towards the strikes of the long Puts. When this happens, falling prices start benefiting the option position. |
| Gamma |
Gamma is slightly negative at initiation but bottoms out at the higher strike, causing the Delta to become more positivewhen the underlying price falls. However, if the price fall continues, Gamma turns positive, causing the Delta to eventually move into the negative zone. Gamma peaks out at the lower strike, causing the Delta to become more negative if the underlying price continues dropping. |
| Vega |
When the underlying price is above the upper breakeven point or below the lower breakeven point, Vega is negative, meaning rising volatility hurts the position, and vice versa. On the other hand, when the underlying price is in between the two breakeven points, Vega is positive, meaning rising volatility benefits the position, and vice versa. |
| Theta |
When the underlying price is above the upper breakeven point or below the lower breakeven point, Theta is positive, meaning time decay benefits the position. On the other hand, when the underlying price is in between the two breakeven points, Theta is negative, meaning time decay hurts the position. |
| Rho |
As Rho is initially positive, rising interest rates can benefit the position, and vice versa. However, once the underlying price falls and moves towards the lower strike price, Rho turns negative because of which rising interest rates start hurting the position, and vice versa. |
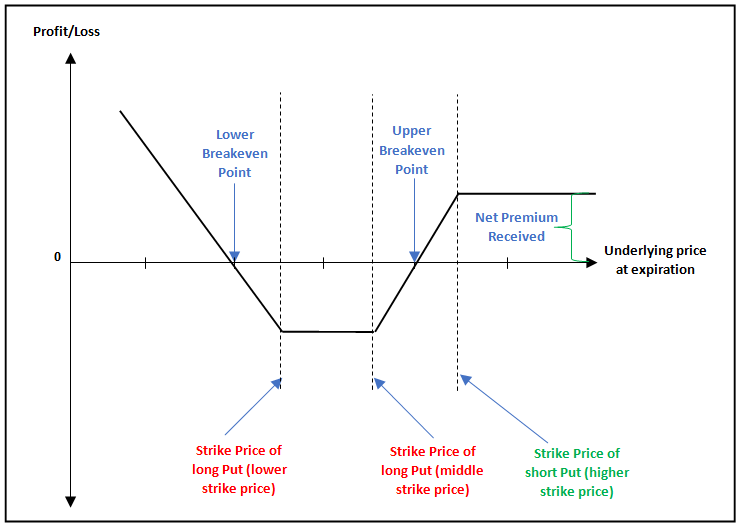
Payoff of Bull Put Ladder
The above is the payoff chart of a Bull Put Ladder strategy. Notice that the strategy is initially neutral to bullish, but it turns bearish when the underlying price drops below the lower strike price. As can be seen, the trader stands to benefit when the underlying price is beyond either of the two breakeven points by expiration and is hurt when the underlying price is between the two breakeven points by expiration. Hence, this strategy must be initiated only when one is either neutral to slightly bullish or is very bearish on the underlying. Also, observe that this strategy has a limited risk and unlimited reward potential.
Example of Bull Put Ladder
Let us say that Mr. ABC, based on his observations on Bank Nifty, has decided to initiate a Bull Put Ladder strategy, wherein he will sell 1 ATM 20000 Put at ₹1,500, buy 1 OTM 19000 Put at ₹700 and another OTM 18500 Put at ₹600. Let us summarize the details of the strategy below:
-
Strike price of shortPut = 20000
-
Strike price of middle longPut = 19000
-
Strike price of lowerlongPut = 18500
-
ShortPut premium (higher strike) = ₹1,500
-
LongPut premium (middle strike) = ₹700
-
LongPut premium (lower strike) = ₹600
-
Net Credit = ₹200 (1500 - 700 - 600)
-
Net Credit (in value terms) = ₹4,000 (200 * 20)
-
Upper breakeven point = 19800 (20000 - 200)
-
Lower breakeven point = 17700 (18500 + 19000 - 20000 + 200)
-
Maximum upside reward = ₹4,000
-
Maximum downside reward = unlimited
-
Maximum risk = ₹16,000 ((20000 - 19000 - 200) * 20)
Now, let us assume a few scenarios in terms of where Bank Nifty would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 25000 | Profit of ₹4,000 | Payoff = [1500-maximum of (20000-25000,0)]+[maximum of (19000-25000,0)-700] + [maximum of (18500-25000,0)-600]. As the underlying price at expiration is above the upper breakeven price, the trader will make a profit |
| 22000 | Profit of ₹4,000 | Payoff = [1500-maximum of (20000-22000,0)]+[maximum of (19000-22000,0)-700] + [maximum of (18500-22000,0)-600]. As the underlying price at expiration is above the upper breakeven price, the trader will make a profit |
| 20000 | Profit of ₹4,000 | Payoff = [1500-maximum of (20000-20000,0)]+[maximum of (19000-20000,0)-700] + [maximum of (18500-20000,0)-600]. As the underlying price at expiration is above the upper breakeven price, the trader will make a profit |
| 19900 | Profit of ₹2,000 | Payoff = [1500-maximum of (20000-19900,0)]+[maximum of (19000-19900,0)-700] + [maximum of (18500-19900,0)-600]. As the underlying price at expiration is above the upper breakeven price, the trader will make a profit |
| 19800 | No profit, No loss | Payoff = [1500-maximum of (20000-19800,0)]+[maximum of (19000-19800,0)-700] + [maximum of (18500-19800,0)-600]. As the underlying price at expiration is equal to the upper breakeven price, the trader will neither make a profit nor incur a loss |
| 19500 | Loss of ₹6,000 | Payoff = [1500-maximum of (20000-19500,0)]+[maximum of (19000-19500,0)-700] + [maximum of (18500-19500,0)-600]. As the underlying price at expiration is below the upper breakeven price, the trader will incur a loss |
| 19000 | Loss of ₹16,000 | Payoff = [1500-maximum of (20000-19000,0)]+[maximum of (19000-19000,0)-700] + [maximum of (18500-19000,0)-600]. As the underlying price at expiration is below the upper breakeven price, the trader will incur a loss |
| 18500 | Loss of ₹16,000 | Payoff = [1500-maximum of (20000-18500,0)]+[maximum of (19000-18500,0)-700] + [maximum of (18500-18500,0)-600]. As the underlying price at expiration is below the upper breakeven price, the trader will incur a loss |
| 18000 | Loss of ₹6,000 | Payoff = [1500-maximum of (20000-18000,0)]+[maximum of (19000-18000,0)-700] + [maximum of (18500-18000,0)-600]. As the underlying price at expiration is below the upper breakeven price, the trader will incur a loss |
| 17700 | No profit, No loss | Payoff = [1500-maximum of (20000-17700,0)]+[maximum of (19000-17700,0)-700] + [maximum of (18500-17700,0)-600]. As the underlying price at expiration is equal to the lower breakeven price, the trader will neither make a profit nor incur a loss |
| 17000 | Profit of ₹14,000 | Payoff = [1500-maximum of (20000-17000,0)]+[maximum of (19000-17000,0)-700] + [maximum of (18500-17000,0)-600]. As the underlying price at expiration is below the lower breakeven price, the trader will make a profit |
| 16000 | Profit of ₹34,000 | Payoff = [1500-maximum of (20000-16000,0)]+[maximum of (19000-16000,0)-700] + [maximum of (18500-16000,0)-600]. As the underlying price at expiration is below the lower breakeven price, the trader will make a profit |
| 15000 | Profit of ₹54,000 | Payoff = [1500-maximum of (20000-15000,0)]+[maximum of (19000-15000,0)-700] + [maximum of (18500-15000,0)-600]. As the underlying price at expiration is below the lower breakeven price, the trader will make a profit |
Observe in the above table that the maximum the trader stands to make when Bank Nifty moves higher for this particular strategy is ₹4,000, which is the net premium that the trader received upfront at the time of strategy initiation. On the other hand, observe that the maximum the trader stands to make when Bank Nifty falls below the lower breakeven price is potentially unlimited - the deeper the fall, the larger the gain. The worst part of this strategy occurs when Bank Nifty gets stuck between the two breakeven points. When such an event occurs, the trader suffers a loss. The good part is that the losses are limited. Notice in the example that the maximum the trader stands to lose under this strategy is ₹16,000.
Next Chapter
Comments & Discussions in
FYERS Community