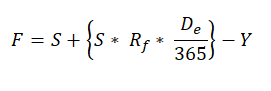By now, we have understood the basic aspects of futures. In the previous three chapters, we have talked about various things such as:
-
What a futures contract is
-
How it is different from a forward contract
-
How the payoff calculation for futures differs from that of forwards
-
Key elements of a futures contract
-
Participants in the futures market, and
-
Instruments available for trading futures in India
We have talked about some vital aspects that are crucialbuilding blocks to understanding futures, such as lot size, total contract value, margins, MTM calculation, price quotation, trading cycle, settlement type, settlement price, expiry, contract rollover etc. Most of these have been talked only briefly, just to introduce these concepts to the reader. In the coming chapters, we will be talking about them in much more detail.
Now that we have a basic level understanding of futures, it is time to dwell a little deeper. In this chapter, we will talk about the pricing of futures contracts. Although it is not an absolute must for a trader to know how the pricing is done, we still advise reading this chapter because knowing how the futures price is calculated would be helpful when deploying advanced strategies using futures, when hedging, understanding whether the futures contract is underpriced or overpriced etc.
Futures price differs from Spot price
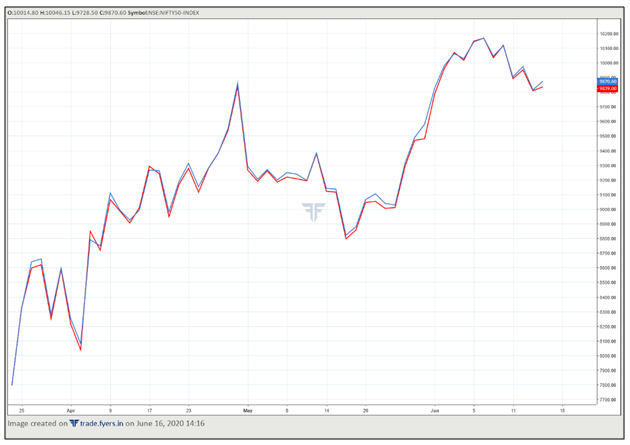
As we know by now, futures price is a derivative of the spot price of the corresponding underlying instrument. For example, the futures price of Nifty is derived from the spot price of Nifty, the futures price of HDFC Bank is derived from the spot price of HDFC Bank, and so on. Because futures price is a derivative of spot price, it tends to closely mimic the spot price. That is, when the spot price rises, the corresponding futures price also rises quite similarly; and when the spot price falls, the corresponding futures price also falls quite similarly.
The chart above compares the spot price of Nifty (blue line) with the futures price of the near-month Nifty June contract (red line). Notice that the two instruments tend to move more or less in sync with each other. However, if you closely observe the two charts, you will see that the two prices are not the same.In fact, if you compare the futures price of any security with its corresponding spot price, you will often notice that there is a price difference between the two.At any point in time, the futures price could be above, equal to, or below the corresponding spot price of the underlying instrument. For instance, look at the screenshot below, taken from the NSE’s website.
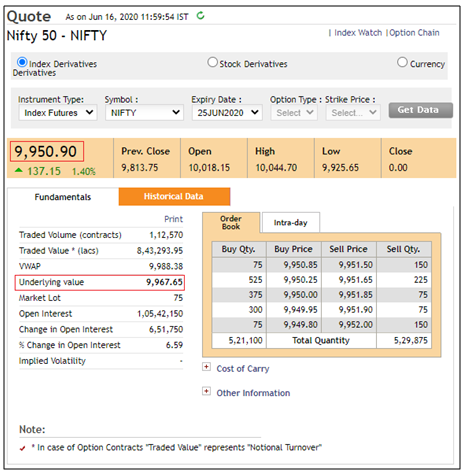
The screenshot above shows the current market statistics of Nifty futures. Notice the box marked in red near the top left of the image. This is the prevailing Nifty futures price for contract that expires in June 2020. Observe that the futures price is currently quoting 9950.90. Now compare the futures price to the underlying price of Nifty, which has been highlighted using another red box below it. Observe that the spot price is currently quoting 9967.65. Notice the difference? As can be seen, the two are different. In this specific case, the futures price is quoting below the spot price.
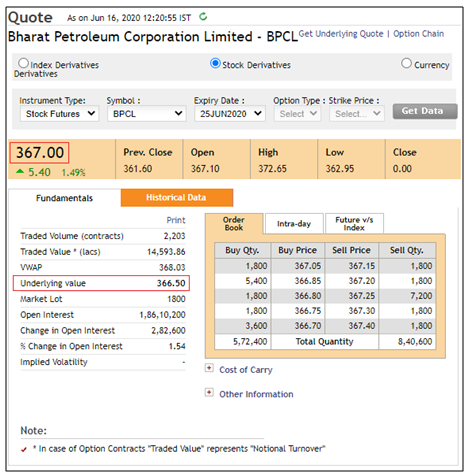
Meanwhile, the above screenshot shows the current market statistics of BPCL futures. Notice here that the futures price of BPCL is trading slightly above its spot price.
Over the course of this chapter, we will talk why the two prices differ, why they tend to converge at expiration of the futures contract, and how the theoretical futures price is calculated from the spot price of the underlying.
Basis
The difference between the spot price and the corresponding futures price is expressedusing a concept calledbasis. Traditionally, basis isexpressed as:
Basis = Spot price of the underlying – Futures price of the same underlying
However, when the underlying and its corresponding futures happen to be a financial asset such as a stock, basis is sometimes expressed as:
Basis = Futures price of the underlying – Spot price of the same underlying
We will largely focus on futures of stocks and equity indices in this chapter and module. Hence, unless otherwise stated, we will use the latter equation for calculating basis.
At any point in time, the basis could be positive, zero, or negative. A positive number means the futures contract is trading at a premium to the corresponding spot price (in commodities, this is called Contango), while a negative number means the futures contract is trading at a discount to the corresponding spot price (in commodities, this is called backwardation). Meanwhile, a value of zero means the futures contract and its corresponding spot price are trading at par.
Over the life of the futures contract, the basis does not remain constant but rather keeps changing with time. It can stay positive, stay negative, move from positive to negative, move from negative to positive etc. When a futures contract is first introduced, the basis usually tends to be wide, primarily because there are a greater number of days to the contract expiration. With time, basis tends to narrow as the expiration of a futures contract approaches. During the life of the futures contract however, depending on the prevailing factors such as demand and supply and the cost of carry, the basis can widen or narrow.
On the day of the expiry of the futures contract, the basis is zero oris very close to zero. In other words, the futures price and the corresponding spot price tend to converge on the day of expiry. If there is a noticeable basis on the day of expiry (positive or negative), an arbitrage opportunity would arise. For instance, if the futures price is noticeably above the spot price on the expiration day, traders would sell in futures and buy in spot. This action would cause the futures price to fall vis-à-vis the spot price and for the basis to disappear. On the other hand, if the futures price is noticeably below the spot price on the expiration day, traders would buy in futures and sell in spot. This action would cause the futures price to rise vis-à-vis the spot price and for the basis to disappear. Of course, such positions would be squared off by expiry once the basis shrinks towards zero and profits are realized.
Basis is an important factor to consider, especially when it comes to hedging. The reason why it is important is because an unexpected strengthening or weakening of basis can benefit or hurt the hedger. We will talk more about basis and basis risk later in this module.
Theoretical Futures Pricing
By now, we know that the spot price and the corresponding futures price tend to vary. In this section, we will talk about a mathematical equation that will enable us to calculate the theoretical futures price of an underlying. Again, in our discussion and examples, we will focus on financial assets (primarily stocks and equity indices) rather than consumable assets (such as commodities).
There are various mathematical models that try to explain the difference between the spot price of an asset and its corresponding futures price. Among these, one of the most widely used pricing model is called the Cost of Carry model. Before we proceed with the mathematical part, let us first try to understand what this model is, in simple terms. The Cost of Carry model measures the total cost of holding anasset over time less any income earned on it during that time. In case of futures, it reflects the costs that one needs to incur for holding a position till the expiration of the futures contract. Another way of looking at this model is to think of it as the additional costs that a seller would incur for purchasing and financing the asset over time. So, in case of futures where the underlying is a stock, the Cost of Carry can be thought ofas interest that is paid to finance the stock. In case any dividend on the stock is expected over the life of the futures contract, it is subtracted from the Cost of Carry.Meanwhile, the costs that are related to holding an asset over time are asset-specific and arise due to one or several factors such as financing costs, transaction costs etc. Meanwhile, in case of commodities, costs such as storage, transportation, and insurance also come into the picture. In brief, think of the Cost of Carry model as the fair theoretical price of futures that is arrived after taking into consideration all the costs and benefits of holding that asset over time.
Theoretically, the futures price is arrived at by adding the cost of carry to the spot price of the underlying. Mathematically, the futures price of an asset, where that asset is a stock can be expressed as follows:
Where,
F = Theoretical Futures price
S = Spot price
Rf = Risk-free rate of interest, per annum
De = Days left to expiration of the futures contract
Y = Dividend
The price derived using the formula above is called the theoretical futures price. The Cost of Carry model is based on certain assumptions, such as:
-
The markets are efficient
-
There are no arbitrage opportunities
-
In case any price inefficiency arises, it is quickly eliminated by arbitrageurs
-
There are no restrictions on borrowing/lending at the risk-free rate
-
The risk-free rate is known with certainty
Now, let us look at a few examples to understand how the theoretical price is calculated on stocks. Having said that, keep in mind that the theoretical futures price and the actual futures price may vary, as the latter is influenced by factors such as the prevailing market forces of demand and supply, market participants factoring potential dividends, etc. By comparing the theoretical futures price with the actual futures price, the trader can get an idea of whether the actual futures price is overvalued or undervalued.
Also, as we can see from the equation mentioned above, we need a fewvalues to calculate the theoretical futures price:
-
Spot price of the corresponding underlying
-
Risk-free rate, per annum
-
Number of days to expiry of the futures contract
-
Dividend, if any
Among these, it is easy to find out the spot price and the number of days left to expiry. But what about the risk-free rate. What rate should be used in the calculation here? Well, one could take the interest rate of government securities, as these tend to be risk-free. Because we are concerned with futures contract having maturities of up to 90days, we willonly consider the 91-day Treasury Bill (T-bill) rate. The prevailing 91-day T-bill rate can be found out on the home page of the RBI’s website, where various prevailing rates are mentioned. At the time of writing, the 91-day T-bill rate is 3.2897%. We will use this figure for our calculation purposes below. In our examples, we shall also assume that the stock won’t be paying dividend over the remaining life of the futures contract. In the real world however, one needs to keep a track of whether a company has declared dividends that would be paid out over the course of the rest of the futures contract’s life. If yes, the same must be subtracted from the calculation because holders of futures contracts don’t receive such benefits.
Example 1: Near-month contract
Let us start by taking the example of Tata Steel. Following are the details of this stock at the time of writing:
-
Futures price = 310.15
-
Spot price = 310.55
-
Risk-free rate = 3.2897%
-
Futures contract Expiry = 25thJune 2020 (near-month)
-
Days to expiry = 8
-
Dividend = 0
Based on the above information, the theoretical futures price can be calculated as:
= 310.55 + {310.55*3.2897%* 8/365} – 0
= 310.77
Example 2: Next-month contract
Let us now calculate the theoretical futures price for Reliance Industries. Following are the details of this stock at the time of writing:
-
Futures price = 1617.00
-
Spot price = 1623.10
-
Risk-free rate = 3.2897%
-
Futures contract Expiry = 30thJuly 2020 (next-month)
-
Days to expiry = 43
-
Dividend = 0
Based on the above information, the theoretical futures price can be calculated as:
= 1623.10 + {1623.10 * 3.2897% * 43/365} – 0
= 1629.39
Example 3: Far-month contract
Let us now calculate the theoretical futures price for SBI. Following are the details of this stock at the time of writing:
-
Futures price = 173.50
-
Spot price = 173.20
-
Risk-free rate = 3.2897%
-
Futures contract Expiry = 27th August 2020 (far-month)
-
Days to expiry = 71
-
Dividend = 0
Based on the above information, the theoretical futures price can be calculated as:
= 173.20 + {173.20 * 3.2897% * 71/365} – 0
= 174.31
An observation that can be made from each of the above three examples is that the theoretical futures price is at premium to the spot price, which is not surprising given that the risk-free rate is positive. However, if you notice, the actual futures price is trading at a discount to the spot price in two out of three cases. This difference is mostly due to the prevailing forces of demand and supply that dictate the futures price. In the next section, we shall try to understand its implication.
Another thing to note is the premium the theoretical futures price commands over the corresponding spot price. For instance, in the first example, the premium was 0.07% (310.77/310.55-1); in the second example, it was 0.39% (1629.39/1623.10-1); while in the third example, it was 0.64% (174.31/173.20-1). Notice that as the number of days to expiration gets larger, the cost of carry also tends to increase. This is because money has a time value component.
Real-world implications of Cost of Carry
Now that we understand the concept and calculation of cost of carry, let us talk about some of its real-world usage and implications. The actual futures price is impacted by the cost of carry as well as by other factors such as the prevailing demand and supply in the market, pricing in possible dividends that a company could pay, etc. If the gap between the actual futures price and the corresponding spot price is widening, it means the cost of carry is rising. Such an action indicates that market participants are willing to pay more to hold the futures contract, which is a bullish indication. On the other hand, if the gap between the actual futures price and the corresponding spot price is narrowing, it means the cost of carry is falling. Such an action indicates that market participants are willing to pay less to hold the futures contract, which is a bearish indication.
Traditionally, when it comes to stocks and equity indices, the actual futures price usually trades at a premium to the corresponding spot price, implying a positive cost of carry. However, occasionally, the actual futures price can also trade at a discount to the corresponding spot price, implying a negative cost of carry. This can happen due to factors such as markets expecting to receive dividend from the company, traders executing arbitrage strategies (such as cash and carry arbitrage wherein traders buy in spot and sell in corresponding futures), etc. Whatever the reason, futures price trading below the corresponding spot price indicates at bearishness among market participants. That said, it is worth reiterating that on the day of expiration, both futures price and the corresponding spot price tend to converge. If they don’t, then arbitrageurs will deploy strategies that would eventually cause prices to converge.
Finally, the difference between the theoretical futures price and the actual futures price can also tell a lot about the prevailing market sentiment and assist one in deploying strategies that could be aimed at taking advantage of such mispricing. Small differences between the two is normal and must usually be ignored. However, if the difference between the two is quite wide, then it gives rise to arbitrage opportunities, which eventually cause the futures price to get back in sync with its fair price. We will talk about such strategies in a much greater detail later in this module.
Next Chapter
Comments & Discussions in
FYERS Community