LONG STRANGLE
| Strategy Details | |
| Strategy Type | Neutral on direction, but bullish on volatility |
| # of legs | 2 (Long OTM Call + Long OTM Put) |
| Maximum Reward | Potentially unlimited |
| Maximum Risk | Limited to the extent of net premium paid |
| Lower Breakeven Price | Put Strike Price - Net Premium Paid |
| Upper Breakeven Price | Call Strike Price + Net Premium Paid |
| Payoff Calculation | Payoff of Long Call + Payoff of Long Put |
Explanation of the Strategy
A Long Strangle is an option strategy wherein the trader would buy 1 OTM, lower strike Put option and simultaneously buy 1 OTM, higher strike Call Option. Both these options must have the same underlying instrument and same expiration date. Just like a Long Straddle, a Long Strangle is also a quite popular multi-legged option strategy among traders because of its limited risk and unlimited reward profile. Both the strategies are similar to each other but have an important distinction, the strike price. Remember that in a Long Straddle, both the options that are bought are ATM options. In a Long Strangle though, the trader would buy OTM options. An advantage of this is that it reduces the overall cost of the strategy. However, a drawback is that it widens the two breakeven points, meaning the underlying will have to travel a longer distance to even breakeven.
By buying a Call and a Put option, the trader is neutral on the direction of the underlying. He/she would stand to benefit from a sharp rise in the underlying price as well as from a sharp fall. Besides a sharp one-sided move in the price of the underlying asset, another factor that is critical to the success of this strategy is volatility. Post initiation, if volatility explodes, the value of the Call and the Put will increase, and vice versa. Hence, execute this strategy when you expect volatility to surge from the time you initiate it. The best time to initiate a Long Strangle is when IVs (Implied Volatility) tend to be comparatively low and you expect them to surge going forward. One can use fundamental parameters to trade this strategy or technical filters to trade this strategy. Irrespective of the parameters used though, the key thing to keep in mind is that when trading this strategy, you outlook on volatility must be very bullish and you must expect the underlying to move sharply, either up or down.
Although this strategy looks quite simple because of its limited risk and unlimited reward potential, be warned that this strategy is far from simple. Although this strategy has a lower overall cost structure as compared to a Long Straddle, keep in mind that for this strategy to even breakeven, the underlying price will have to travel an even greater distance as compared to a Long Straddle. Also remember that because both the options are long options, time decay will act as a major headwind. Hence, the odds are notably stacked against the trader when it comes to making money using this strategy.
Maximum loss under this strategy is limited to the extent of net premium paid and occurs when the underlying price is somewhere between the two strikes on expiration. On the other hand, maximum profit is potentially unlimited and occurs when the underlying price rises sharply or falls sharply. If the underlying price rises sharply, the Put will become worthless and the Call will start becoming profitable. On the other hand, if the underlying price falls sharply, the Call will become worthless and the Put will start becoming profitable. This strategy has two breakeven points, lower and upper. For the strategy to become profitable, the underlying price will have to either rise above the upper breakeven point or fall below the lower breakeven point.
Benefits of the Strategy
-
This strategy has risk that is limited to the extent of net premium paid
-
This strategy has a potential for unlimited reward
-
This strategy can profit from either side move in the price of the underlying instrument, provided the move is substantial
-
Compared to a Long Straddle, this strategy costs less
Drawbacks of the Strategy
-
This is a net debit strategy because of the two options that are purchased
-
There is a possibility that the trader could lose 100% of his/her investment if the underlying price is somewhere between the two strikes on expiration
-
Because both the options are long, time decay is the biggest enemy of this strategy
-
If volatility does not pick up or if the underlying price stays range bound, time decay would erode the values of both the options
Strategy Suggestions
-
Ensure that your view on volatility is very bullish
-
Ensure that you expect the underlying instrument to trend strongly in one direction, up or down
-
Avoid executing this strategy on instruments that do not move much or have historically low volatility, such as low Beta type stocks. Instead, use this strategy on instruments that have historically exhibited high volatility, such as high Beta stocks
-
Use technical or fundamental parameters when trading this strategy
-
Looks for consolidation patterns such as flags, pennants, Bollinger squeeze etc. on the charts as moves out of such patterns are usually followed by sharp move in the direction of the breakout
-
Before executing this strategy, look out at the IVs of both the options as initiating this strategy when IVs are remarkably high would not only increase the cost of the strategy but could also pose the risk of IVs cooling off post initiation (as IVs tend to be mean reverting)
-
If the premiums of the options are declining and if expiration is soon approaching, consider exiting the strategy as time decay tends to accelerate near to expiration
-
Frequently keep a track of IVs and the trend of the underlying instrument
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Long Strangle
| Greek | Notes |
| Delta |
Delta is at or close to zero at initiation. If the underlying price rises above the midpoint of the two strikes, Delta starts rising above zero. The higher the rise in the underlying, the higher the rise in Delta above zero as the Call becomes ITM and the Put remains OTM. Meanwhile, if the underlying drops below the midpoint of the two strikes, Delta starts falling below zero. The larger the drop in the underlying, the more will the Delta fall below zero as the Put becomes ITM and the Call remains OTM. |
| Gamma |
As both the options have positive Gamma values, Gamma tends to be somewhere near its peak at initiation. When Gamma is at its peak, the position Delta tends to be most sensitive to changes in the underlying price. As the underlying price starts moving outside the two strikes, Gamma starts to decline and move towards zero, meaning the impact of Gamma on Delta starts reducing. |
| Vega |
As both the options have positive Vega values, Vega tends to be closer to its peak at initiation. As a result, the impact of change in IVs tends to be the greatest between the two strikes. As the underlying price starts moving outside the two strikes, Vega starts to decline and move towards zero, meaning the impact of changes in IVs on option premiums gradually starts tapering off. |
| Theta |
As both the options have negative Theta values, Theta tends to be closer to its most negative at initiation. As a result, time decay has the greatest negative impact between the two strikes. However, as the underlying starts moving outside the two strikes, Theta starts to increase and move towards zero, meaning the negative impact of time decay on option premiums gradually starts tapering off. |
| Rho |
Rho is around zero at initiation. As the underlying price rises above the higher strike, Rho rises and moves above zero, meaning rising interest rates benefit the position, and vice versa. On the other hand, as the underlying falls below the lower strike, Rho drops and moves below zero, meaning rising interest rates hurt the position. That said, this is the least significant of the five option Greeks. |
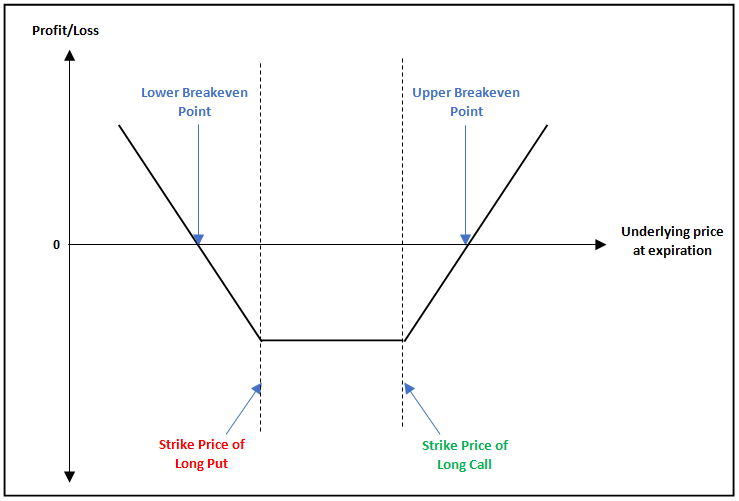
Payoff of Long Strangle
The above is the payoff chart of a Long Strangle strategy. Notice that this strategy is executed by buying an OTM Put option and an OTM Call option. See that for the strategy to achieve breakeven, the underlying price will have to either rise above the upper breakeven point or fall below the lower breakeven point. Until that happens, the trader would be in a loss-making position. Observe that beyond either of the two breakeven points, profit can be potentially unlimited. Meanwhile, see that maximum loss under this strategy occurs when the underlying price is anywhere between the two strikes at expiration.
Example of Long Strangle
Let us say that Mr. ABC has decided to execute a Long Strangle strategy on JSW Steel. The details of the strategy are as below:
-
Strike price of OTM long Put = 160
-
Strike price of OTM long Call = 170
-
Long Put premium = ₹2.45
-
Long Call premium = ₹3.40
-
Net Debit = ₹5.85 (2.45 + 3.40)
-
Net Debit (in value terms) = ₹13,455 (5.85 * 2300)
-
Lower Breakeven point = 154.15 (160 - 5.85)
-
Upper Breakeven point = 175.85 (170 + 5.85)
-
Maximum reward = Unlimited
-
Maximum risk = ₹13,455
Now, let us assume a few scenarios in terms of where JSW Steel would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 130 | Profit of ₹55,545 | Payoff = [Maximum of (130-170,0)-3.40] + [Maximum of (160-130,0)-2.45]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 140 | Profit of ₹32,545 | Payoff = [Maximum of (140-170,0)-3.40] + [Maximum of (160-140,0)-2.45]. As the underlying price at expiration is below the lower breakeven point, the trader will make a profit |
| 154.15 | No profit, No loss | Payoff = [Maximum of (154.15-170,0)-3.40] + [Maximum of (160-154.15,0)-2.45]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 158 | Loss of ₹8,855 | Payoff = [Maximum of (158-170,0)-3.40] + [Maximum of (160-158,0)-2.45]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 160 | Loss of ₹13,455 | Payoff = [Maximum of (160-170,0)-3.40] + [Maximum of (160-160,0)-2.45]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 165 | Loss of ₹13,455 | Payoff = [Maximum of (165-170,0)-3.40] + [Maximum of (160-165,0)-2.45]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 170 | Loss of ₹13,455 | Payoff = [Maximum of (170-170,0)-3.40] + [Maximum of (160-170,0)-2.45]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 172 | Loss of ₹8,855 | Payoff = [Maximum of (172-170,0)-3.40] + [Maximum of (160-172,0)-2.45]. As the underlying price at expiration is between the two breakeven points, the trader will incur a loss |
| 175.85 | No profit, No loss | Payoff = [Maximum of (175.85-170,0)-3.40] + [Maximum of (160-175.85,0)-2.45]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 190 | Profit of ₹32,545 | Payoff = [Maximum of (190-170,0)-3.40] + [Maximum of (160-190,0)-2.45]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
| 200 | Profit of ₹55,545 | Payoff = [Maximum of (200-170,0)-3.40] + [Maximum of (160-200,0)-2.45]. As the underlying price at expiration is above the upper breakeven point, the trader will make a profit |
Notice in the above table that if JSW Steel falls below the lower BEP of 154.15 or rises above the upper BEP of 175.85, the trader starts to make money on the strategy. See that the profit gets bigger and bigger, the more the JSW Steel falls below 154.15 or rises above 175.85. On the flip side, notice that if the underlying price gets stuck within the two breakeven points, the trader will suffer a loss. Observe that maximum loss of ₹13,455 occurs if JSW Steel is somewhere between the two strikes of 160 and 170 on expiration, in which case both the options expire worthless.
SHORT STRANGLE
| Strategy Details | |
| Strategy Type | Neutral on direction, but bearish on volatility |
| # of legs | 2 (Short OTM Call + Short OTM Put) |
| Maximum Reward | Limited to the extent of net premium received |
| Maximum Risk | Potentially unlimited |
| Lower Breakeven Price | Put Strike Price - Net Premium Received |
| Upper Breakeven Price | Call Strike Price + Net Premium Received |
| Payoff Calculation | Payoff of Short Call + Payoff of Short Put |
Explanation of the Strategy
A Short Strangle is a strategy wherein the trader would sell an OTM Put and simultaneously sell an OTM Call. Both these options must have the same underlying instrument and expiration date. This strategy is quite similar to a Short Straddle but has an important distinction, the strike price. Recollect that in a Short Straddle, both the options sold are ATM options. In a Short Strangle though, both the options sold are OTM options. A Short Strangle has advantages and disadvantages over a Short Straddle. An advantage is that the breakeven points are wider, meaning the underlying price will have to travel a greater distance for the trader to start incurring losses. Also, the maximum profit zone would be wider compared to a Short Straddle, in which the maximum profit zone is restricted to just one point. On the other hand, a disadvantage is that this strategy will have a smaller net credit compared to a Short Straddle.
By selling a Call and a Put at different strikes, the trader expects the underlying instrument to stay range bound and hover between the two strikes for the remainder of the option’s life. The trader would also expect IVs to reduce post the initiation of this strategy, as this would reduce the values of the two options. Hence, it can be said that a trader would implement this strategy when he expects the underlying to remain range bound and IVs to contract. Given that IVs tend to be mean reverting, traders sometime prefer initiating this strategy when IVs are abnormally high, hoping that they would shrink going forward and return to normal levels.
A Short Strangle is a net credit strategy. If implemented correctly under right market conditions, this strategy can be a good source of income. However, it must be kept in mind that this strategy is an advanced option strategy because of its risk reward profile. It must be kept in mind that the profitability starts reducing as the underlying price moves outside the zone of the two strikes. Meanwhile, if the underlying price falls or rises beyond a certain point, the trader starts suffering losses, which can get catastrophic. Hence, care must be taken when initiating this strategy. Preferably, this strategy must be executed by experienced option traders only.
A Short Strangle has two breakeven points, lower and upper. The strategy is profitable as long as the underlying price is inside the range of the two breakeven points. Maximum profit under this strategy is limited to the extent of net premium received and occurs when the underlying price is anywhere between the two strikes at expiration. On the other hand, maximum loss under this strategy is unlimited and occurs when the underlying price either falls below the lower breakeven or rises above the upper breakeven. The larger the decline in the underlying price below the lower breakeven point or the larger the rise in the underlying price above the upper breakeven point, the larger will be the trader’s losses.
Benefits of the Strategy
-
This strategy is a net credit strategy
-
This strategy can be a good source of income if used under right market conditions
-
For this strategy, time decay is immensely beneficial
-
Compared to a Short Straddle, this strategy has a wider maximum profit zone
-
Compared to a Short Straddle, this strategy has wider breakeven points
Drawbacks of the Strategy
-
This strategy has an unlimited risk profile
-
This strategy has a limited reward profile
-
Compared to a Short Straddle, this strategy has a smaller net credit
-
An unexpected rise in volatility would be detrimental to the success of the strategy
-
Any unexpected price-sensitive news or event could spell big trouble to the trader
Strategy Suggestions
-
Ensure that your view on the underlying is range bound and your view on volatility is bearish
-
When executed, keep a regular track of both the options
-
Preferably, avoid this strategy on instruments that tend to be extremely volatile, such as high beta stocks. Instead, implement this strategy on instruments that have historically seldom exhibited huge volatility
-
Before executing this strategy, look out at the IVs of both the options as initiating this strategy when IVs are very low would not only mean a smaller net credit but could also pose the risk of IVs rising (as IVs tend to be mean reverting)
-
Avoid executing this strategy ahead of the announcement of a price-sensitive data or event
-
If already holding a position ahead of a price-sensitive data or event, consider exiting it, especially if the event is lined up outside of market hours
-
Frequently keep a track of IVs and the trend of the underlying instrument to ensure that there are no surprises/shocks
-
Because you are short both the options, give yourself as little time to go wrong as possible. In other words, execute this strategy when expiration is not far away
-
Ensure there is sufficient liquidity in the underlying that is being chosen to initiate this strategy
Option Greeks for Short Strangle
| Greek | Notes |
| Delta |
Delta is at or close to zero at initiation. If the underlying price rises above the midpoint of the two strikes, Delta starts falling below zero. The higher the rise in the underlying, the lower the Delta falls below zero. Meanwhile, if the underlying drops below the midpoint of the two strikes, Delta starts rising above zero. The larger the drop in the underlying, the higher the Delta rises above zero. |
| Gamma |
As both the options have negative Gamma values, Gamma tends to be near its most negative at initiation. As a result, Delta tends to be most sensitive to changes in the underlying price around the midpoint of the two strikes. As the underlying price starts moving outside the two strikes, Gamma starts to rise and move towards zero, meaning the impact of Gamma on Delta starts tapering off. |
| Vega |
As both the options have negative Vega values, Vega tends to be near its most negative at initiation. As a result, the impact of change in IVs tends to hurt the most around the midpoint of the two strikes. As the underlying price starts moving outside the two strikes, Vega starts to rise and move towards zero, meaning the impact of changes in IVs on option premiums gradually starts tapering off. |
| Theta |
As both the options have positive Theta values, Theta tends to be near its peak at initiation. As a result, time decay has the greatest positive impact around the midpoint of the two strikes. However, as the underlying starts moving outside the two strikes, Theta starts to reduce and move towards zero, meaning the positive impact of time decay on option premiums gradually starts tapering off. |
| Rho |
Rho is around zero at initiation. As the underlying price rises above the midpoint of the two strikes, Rho falls and moves below zero, meaning rising interest rates hurt the position, and vice versa. On the other hand, as the underlying falls below the midpoint of the two strikes, Rho rises and moves above zero, meaning rising interest rates benefit the position, and vice versa. That said, this is the least significant of the five option Greeks. |
Payoff of Short Strangle
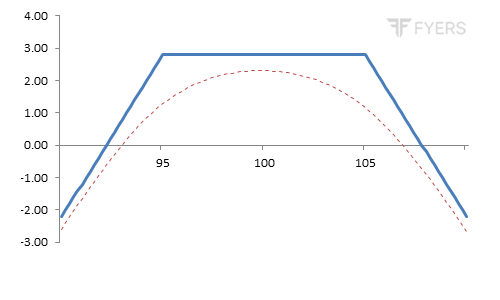
The below is the payoff chart of a Short Strangle strategy. Notice that this strategy is executed at OTM strikes. See that this strategy achieves its maximum profit potential when the underlying price is anywhere between the two strikes at expiration. As the underlying price starts moving outside the two strikes, the profitability starts reducing. Observe that the strategy remains profitable as long as the underlying price is inside the range of the two breakeven points. As the underlying price moves outside the range of one of the two breakeven points, the trader starts incurring losses. See that the larger the drop in the underlying price below the lower breakeven point or the larger the rise above the upper breakeven point, the greater will be the trader’s loss.
Example of Short Strangle
Let us say that Mr. ABC has decided to execute a Short Strangle strategy on HDFC Bank. The details of the strategy are as below:
-
Strike price of OTM short Put = 820
-
Strike price of OTM short Call = 860
-
Short Put premium = ₹9
-
Short Call premium = ₹11
-
Net Credit = ₹20 (9 + 11)
-
Net Credit (in value terms) = ₹10,000 (20 * 500)
-
Lower Breakeven point = 800 (820 - 20)
-
Upper Breakeven point = 880 (860 + 20)
-
Maximum reward = ₹10,000
-
Maximum risk = Unlimited
Now, let us assume a few scenarios in terms of where HDFC Bank would be on the expiration date and the impact this would have on the profitability of the trade.
| Underlying price at Expiration | Net Profit/Loss | Notes |
| 700 | Loss of ₹50,000 | Payoff = [11-Maximum of (700-860,0)] + [9-Maximum of (820-700,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 750 | Loss of ₹25,000 | Payoff = [11-Maximum of (750-860,0)] + [9-Maximum of (820-750,0)]. As the underlying price at expiration is below the lower breakeven point, the trader will incur a loss |
| 800 | No profit, No loss | Payoff = [11-Maximum of (800-860,0)] + [9-Maximum of (820-800,0)]. As the underlying price at expiration is equal to the lower breakeven point, the trader will neither make a profit nor incur a loss |
| 810 | Profit of ₹5,000 | Payoff = [11-Maximum of (810-860,0)] + [9-Maximum of (820-810,0)]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 820 | Profit of ₹10,000 | Payoff = [11-Maximum of (820-860,0)] + [9-Maximum of (820-820,0)]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 840 | Profit of ₹10,000 | Payoff = [11-Maximum of (840-860,0)] + [9-Maximum of (820-840,0)]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 860 | Profit of ₹10,000 | Payoff = [11-Maximum of (860-860,0)] + [9-Maximum of (820-860,0)]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 870 | Profit of ₹5,000 | Payoff = [11-Maximum of (870-860,0)] + [9-Maximum of (820-870,0)]. As the underlying price at expiration is between the two breakeven points, the trader will make a profit |
| 880 | No profit, No loss | Payoff = [11-Maximum of (880-860,0)] + [9-Maximum of (820-880,0)]. As the underlying price at expiration is equal to the upper breakeven point, the trader will neither make a profit nor incur a loss |
| 1000 | Loss of ₹60,000 | Payoff = [11-Maximum of (1000-860,0)] + [9-Maximum of (820-1000,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
| 1200 | Loss of ₹160,000 | Payoff = [11-Maximum of (1200-860,0)] + [9-Maximum of (820-1200,0)]. As the underlying price at expiration is above the upper breakeven point, the trader will incur a loss |
Notice in the above table that the trader makes a profit only if HDFC Bank is trading within the range of the two breakeven points - 800 and 880. See that maximum profit is limited to the extent of net credit received - ₹10,000 - and occurs when HDFC Bank is anywhere between the two strikes of 820 and 860 on expiration. Meanwhile, observe that if HDFC Bank falls below 800 or rises above 880, the trader starts suffering losses. The more HDFC Bank falls below 800 or rises above 880, the greater will be the trader’s loss, which can get potentially catastrophic if the position is held onto.
Next Chapter
Comments & Discussions in
FYERS Community